En la siguiente animación podéis ver como construye una araña su telaraña. Una muestra más de que la geometría está presente en la naturaleza.
L’araignée tisse sa toile por Espacedessciences
Podemos observar como usando triángulos (es el único polígono indeformable) construye la base de la telaraña con el objetivo de tener una estructura rígida y resistente. Una vez hecha la estructura base, pasa a construir mediante elipses el resto de la telaraña, consiguiendo una estructura trampa certera.
Para finalizar, la araña se va al centro de la telaraña para detectar cualquier vibración que se produzca.
Y si queréis ver a una araña real en acción, os dejo este precios vídeo:
Timelapse: une araignée tisse sa toile from Jean-Michel Niester on Vimeo.
Os dejo un libro interactivo hecho en Geogebra que sirve de introducción a la trigonometría de forma visual. Con dicho interactivo podéis experimentar todos los conceptos mediante la manipulación de figuras. Es un excelente recurso para visualizar y comprender la trigonometría.
En el libro podéis experimentar con:
- Razones trigonométricas fundamentales: seno, coseno y tangente de un ángulo agudo.
- Circunferencia goniométrica o trigonométrica. Representación de ángulos en la circunferencia. Extensión de las razones trigonométricas a ángulos mayores de 90º.
- Relaciones entre ángulos de diferentes cuadrantes:
- ángulos complementarios: suman 90º
- ángulos suplementarios: suman 180º
- ángulos que difieren en 180º
- ángulos que suman 360º y ángulos opuestos
- Aplicaciones de la semejanza de triángulos.
- Resolución de triángulos rectángulos y cálculo de áreas
- Cálculo de alturas y distancias
Para acceder al libro pincha en la siguiente imagen:
Llevo dos años manteniendo y actualizando la web que quiero compartir con vosotros: «Matemáticas en la ESO«. Esta web trata de ser un libro digital de las diferentes asignaturas de matemáticas de la ESO.
De momento, solo hay contenidos de 1º y 2º de la ESO y algunos temas de 4º ESO B, en años sucesivos iré completando los materiales hasta conseguir tener los libros digitales de los cuatro cursos y actualizarlos a la LOMCE.
En dicha web, todos los cursos están divididos en temas que tratan de seguir los contenidos que marca el currículo de la LOE.
Dentro de cada tema existen, como mínimo, las siguientes secciones:
- Teoría: todos los contenidos del tema y, en algunos de ellos, un resumen o esquema del tema.
- Observa cómo se hace: basado en las ideas de Khan Academy, en esta sección encontraréis una recopilación de vídeos creados por diferentes profesores que explican los principales procedimientos que se trabajan en el tema. Un buen recurso que puede hacer la función de un profesor particular.
- Practica tú mismo: encontraréis una recopilación de las mejores actividades interactivas que he encontrado sobre los diferentes temas y que permiten practicar los contenidos de forma autónoma con la posibilidad de autoevaluarse.
- Ejercicios y problemas: una recopilación de las clásicas hojas de ejercicios y problemas para poder descargarlas y trabajarlas. Muchas de ellas están con las soluciones.
En algunos temas, he publicado libros interactivos hechos en Geogebra que permiten ver los contenidos del tema de una forma más visual e interactiva.
También existe una sección dedicada a algunas actividades que he realizado con mis alumnos en el Taller de matemáticas. Por ejemplo, podéis hacer una visita al trabajo de la geometría con papiroflexia: «Geometría con origami»
Espero vuestra opinión.
En este segundo trimestre, estamos trabajando la semejanza de figuras, en particular, la de triángulos y por supuesto el famoso teorema de Tales. Una de las principales aplicaciones del teorema de Tales es la medición de objetos de gran altura. En breves días, os compartiré una actividad al aire libre que hemos hecho en 4º de ESO consistente en medir alturas alrededor del instituto junto a os instrumentos caseras que hemos usado para tal menester y la creación de dichos instrumentos.
Lo que os quiero mostrar en esta entrada, son las posibilidades del programa Geogebra para visualizar este tipo de problemas geométricos y, de esta forma, nos sea más sencillo realizar las actividades.
Uno de los métodos que hemos comentado en clase y que de no haber sido por la lluvia hubiéramos usado en la actividad, es el que nos muestra Julio Verne en su libro «La isla misteriosa» y que os pongo a continuación tal y como nos cuenta Yákov Perelmán en su libro «Geometría Recreativa«:
– Hoy vamos a medir la altura del acantilado de Vista Lejana, –dijo el ingeniero.
– ¿Necesitamos algunos instrumentos? –preguntó Gebert.
– No hace falta. Lo haremos de otra manera, más fácil y más segura.
El joven, caminó desde el acantilado hasta la orilla. Cogió un jalón de 12 pies de
longitud, el ingeniero comprobó la medida con su estatura, la cual conocía bien.
Gebert entregó una plomada al ingeniero; ésta no era más que una piedra atada al
extremo de una cuerda. Situándose a 500 pies del acantilado vertical, el ingeniero
clavó el jalón verticalmente en la arena, con la ayuda de la plomada, enterrándola a
dos pies de profundidad. Luego se alejó del jalón, hasta que tumbándose en el suelo
pudo ver el extremo saliente del jalón y la cresta del acantilado en línea recta
(Figura 7). Marcó este punto con una estaca.
– ¿Tienes algunas nociones de geometría?– preguntó a Gebert.
– Sí.
– ¿Recuerdas las propiedades de los triángulos semejantes?
– Sus lados correspondientes son proporcionales.
– Exacto. Ahora voy a construir dos triángulos rectángulos semejantes. Un cateto
del triángulo pequeño será el jalón, el otro cateto, será la distancia desde la estaca
hasta el pie del jalón; la hipotenusa, es mi línea de vista. En el triángulo mayor los
catetos son el acantilado, cuya altura queremos medir, y la distancia desde la
estaca hasta el pie del acantilado; la hipotenusa es mi línea de vista, que se une con
la hipotenusa del triángulo menor.
– ¡He entendido! – exclamó el joven. La distancia de la estaca hasta el jalón es a la
distancia desde la estaca hasta el pie del acantilado, como la altura del jalón es a la
altura del acantilado.
– Exactamente. Sigamos, si medimos las dos primeras distancias, y sabemos la
altura del jalón, podemos calcular el cuarto miembro de la proporción que es la
altura del acantilado.
Se midieron ambas distancias horizontales: la pequeña midió 15 pies, la grande
midió 500 pies.
Finalmente el ingeniero anotó:
15 : 500 = 10 : x
15 x = 500 x 10
x=333,3 pies
Entonces, la altura del acantilado es de 333 pies.«Geometría Recreativa» de Yákov Perelmán
Para poder visualizar este método y los demás que hemos usado, he creado unas aplicaciones interactivas con Geogebra con las que se puede visualizarlos y entender mejor los procedimientos.
El objetivo final es crear un libro interactivo que muestre las principales aplicaciones del Teorema de Tales.
Hasta que llegue ese momento y a ,modo de aperitivo, os comparto dos geogebras que he creado para describir el método de Julio Verne.
Debéis mover los tiradores verdes para entender el método. Os recomiendo que mováis los tiradores con el teclado, se consigue mucha más precisión.
- Cálculo de la altura de un edificio (Julio Verne-simplifica)
- Método de calcular alturas de Julio Verne. Versión ampliada
Espero que os gusten ;-).
Fuente de la imagen de Tales de Mileto: «Illustrerad Verldshistoria band I Ill 107» por Ernst Wallis et al – own scan. Disponible bajo la licencia Dominio público vía Wikimedia Commons.
Esta es la tercera curiosidad numérica que publico en el blog relacionada con el número 9. ¿Por qué será?
Otras curiosidades del 9:
Para las fiestas del instituto vamos a hacer una gran zumo de frutas. Como no sabemos las cantidades necesarias, le hemos preguntado a Fibonacci, cocinero del restaurante del instituto. Fibonacci que es un gran amante de las matemáticas nos ha dado las cantidades de la siguiente forma:
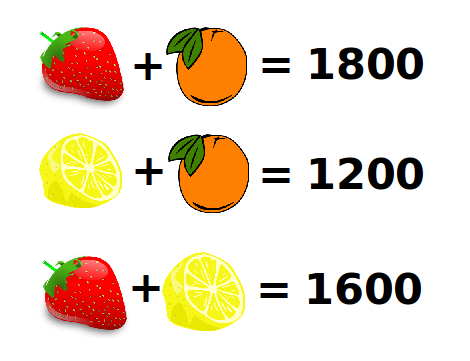
¿Nos ayudas a descifrar la receta?










Comentarios recientes