Os comparto otra curiosidad numérica en forma de pirámide, en este caso del número 9:
El conocer la historia de las matemáticas puede ser la mejor forma de conocer el desarrollo de la ciencia y del pensamiento humano. Pero no os quiero hablar de todo eso, simplemente quiero compartir con vosotros un bonito recurso creado por el ya extinto programa «Internet en el aula«.
Un recurso que muchos conoceréis pero no por ello deja de ser interesante. Una historia interactiva de las matemáticas en cómic que puede servir tanto para último ciclo de primaria como secundaria.
Os animo a que la veáis y admiréis la belleza de esta disciplina:
Al empezar a ver las áreas de las principales figuras planas: rectángulo, triángulo, trapecio, rombo, etc, prefiero perder más tiempo en la deducción de dichas áreas o, cuanto menos, en darles más sentido a las fórmulas. De otra manera aprenden memorísticamente sin entender para nada lo que quieren decir las fórmulas, una vez más, nos saltamos el paso de lo concreto a lo abstracto.
Para la deducción de dichas fórmulas, tenemos diferentes posibilidades que todas ellas parten de la idea que debe quedar clara de que todas las fórmulas emanan de la más intuitiva: la del rectángulo.
Trabajo con el Geoplano
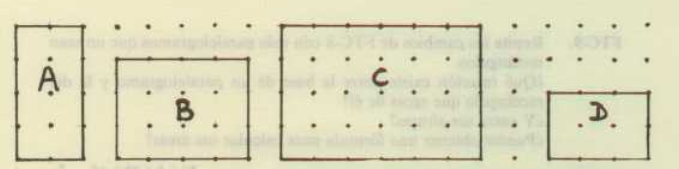
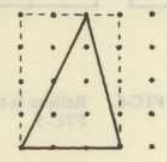
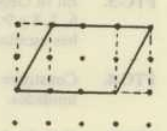
Podemos empezar a trabajar las áreas de los rectángulos con diferentes actividades sobre un geoplano ortométrico de trama cuadriculada:

Debido a la sencillez de la construcción de las figuras, podemos trabajar a la vez, el perímetro y las áreas de los rectángulos, de los triángulos, trapecios, etc.
Si tomamos como unidad de medida el área de un cuadrado pequeño, podemos plantear diferentes retos para que deduzcan las áreas de diferentes figuras: pueden ser rectángulos, triángulos, trapecios, polígonos convexos, etc.
En las siguientes imágenes podéis ver diferentes propuestas que os pueden ser útiles:
Trabajo con Geogebra
A la par o después de haber hecho diferentes actividades, podemos trabajar con Geogebra para experimentar la deducción de las diferentes fórmulas.
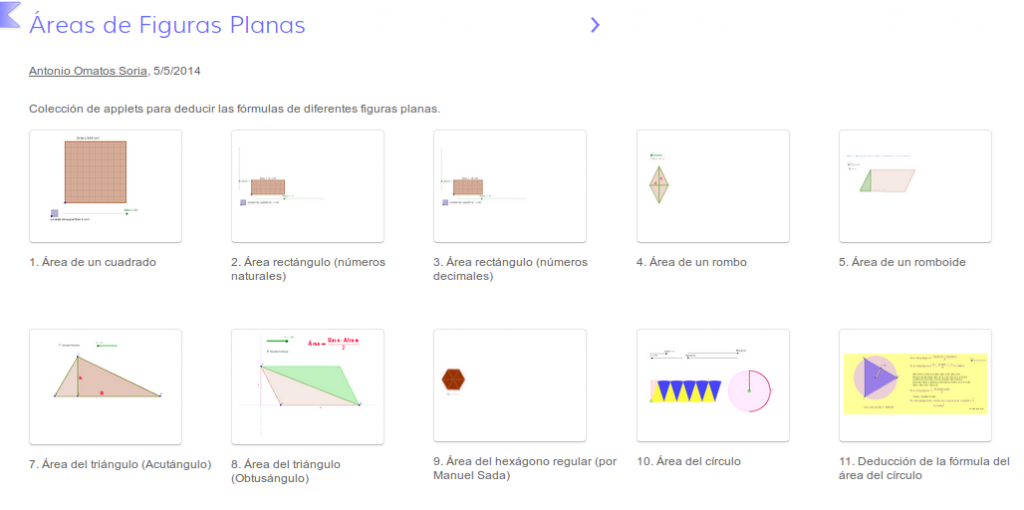
Con este motivo he creado un libro interactivo en Geogebra para experimentar con el razonamiento de las fórmulas de las principales figuras planas. Podemos comprobar como surgen las fórmulas de las principales figuras planas: cuadrado, rectángulo, rombo, romboide, triángulo, polígonos regulares, área del círculo y longitud de la circunferencia:
La gran mayoría de los interactivos que componen el libro son de creación propia, excepto los tres últimos que son de dos cracks del geogebra: Manuel Sada y de Juan carlos Mora. Desde aquí quiero agradecerles su trabajo.
Que las identidades notables les resultan difíciles a los alumnos es un hecho. Por este motivo trato de enseñarlas desde diferentes enfoques para ver si consigo que acaben de verles algo de sentido. Desde mi punto de vista el principal sentido de las identidades notables es verlas de derecha a izquierda.
Me parece importante realizar primero operaciones numéricas que simulen las principales identidades notables:
- (7+4)² y similares. Muchos alumnos tienen la tendencia a hacer 7² + 4²
- 18·22. Aquí les planteo el truco de la diferencia de cuadrados para hacer los cálculos mentales. Jugamos un rato en hacer cálculos de este tipo de forma más rápida.
Luego pasamos a hacer las multiplicaciones de polinomios (binomios) del tipo:
- (x+2)(x+2), (x-3)(x-3),…
- (x+2)(x-2), ….
Y antes de llegar a la fórmula vemos la visión geométrica. La mayoría de las veces, la hacemos con un cuadrado de papel. Luego, las vemos con ayuda de la siguiente presentación:
Para la última sesión antes de navidades, en 2º de ESO, hago una gymkana algebraica que tiene como premio unas chuches.
Divido a la clase en seis grupos de cuatro o cinco alumnos.
Cada grupo debe resolver unos problemas algebraicos que les darán unos códigos.
A cada grupo que resuelve el código correctamente se le da alguna palabra del enigma final.
El objetivo es resolver el enigma final con las palabras de todos los grupos: «Os deseo unas felices vacaciones llenas de polinomios 😉»
Os dejo los materiales de la actividad por si queréis llevarla a cabo:
«Si no puedes resolver un problema, entonces hay una manera más sencilla de resolverlo: encuéntrala» George Polya
Que el juego es un potente elemento de aprendizaje creo que no le cabe duda a nadie. Y si hay una disciplina dónde existen múltiples juegos, ésta es las matemáticas. Me vienen las palabras del maestro Miguel de Guzmán al respecto:
“El juego y la belleza están en el origen de una gran parte de la matemática. Si losmatemáticos de todos los tiempos se la han pasado tan bien jugando y han disfrutadotanto contemplando su juego y su ciencia, ¿por qué no tratar de aprender la matemáticaa través del juego y de la belleza?”
Considero que a través de los juegos de matemáticas podemos:
- Divertirnos que no es poco
- Manipulación autónoma por los estudiantes
- Una rápida familiarización con la situación y sus dificultades
- Ensayos diversos y diferentes por los estudiantes
- Investigar pautas y comportamientos en el juego
- Analizar reglas y estrategias para jugar mejor lo que supone elaborar las estrategias posibles y elegir de entre ellas.
- …
Si nos fijamos en todo lo anterior, podemos ver que están presentes los cuatro pasos (*) para resolver problemas que Polya nos dejó :
- Entender el problema.
- Configurar un plan
- Ejecutar el plan
- Mirar hacia atrás
Al igual que Polya pienso que el aprendizaje en base a la resolución de problemas es el recurso más potente que tenemos para el aula de matemáticas. Sin embargo, la presión del currículo, con sus excesivos contenidos, su orientación hacia el bachillerato y sus criterios de evaluación conllevan el tener que trabajar muchas veces de forma más mecánica. Esta forma de trabajar, añade más abstracción (nos olvidamos de pasar de lo Concreto a lo Abstracto CP) con lo que se otorga mayor dificultad a las matemáticas.
Por otro lado, también tenemos que luchar contra las muchas resistencias a la asignatura (la gran mayoría de los alumnos me llegan a primero con el mantra bien aprendido de que no les gustan las matemáticas, ¿comorrr?). A modo de ejemplo, os pongo un tuit que publiqué con una anécdota que me sucedió la semana pasada y que muestra muy bien lo que quiero decir:
Con objeto de romper todo lo que anteriormente he nombrado, de vez en cuando, aproximadamente cada 15 días, hacemos una sesión de problemas abiertos. Sesión que les gusta mucho, en la que nos dividimos en parejas, grupos de tres o de cuatro personas y nos ponemos a resolver problemas abiertos. Para mi problemas abiertos, son aquellos que se pueden resolver con un buen razonamiento matemático y para los que no es necesario tener muchos conocimientos de matemáticas.
Os comparto algunos de los juegos de estrategia que he usado con los alumnos dentro de dichas sesiones. En concreto, son juegos de estrategia ganadora que son muy motivantes y que les suponen un reto, sobre todo cuando ven que les gano siempre ;-):
Espero que os gusten y espero vuestras opiniones y aportaciones.
(*) Aquí tenéis una presentación que muestra el método de Polya
En este caso os voy a mostrar el método que uso al iniciar los diferentes temas. Trato de que vean el tema desde la aplicación en la vida cotidiana para posteriormente si no queda otro remedio pasar a la parte más abstracta. Viene a definirse como CPA (de lo Concreto a lo Pictórico y posteriormente a lo Abstracto), algunas veces lo dejo en CA (de lo Concreto a lo Abstracto)
Por ejemplo al empezar con las inecuaciones, tenemos dos posibilidades:
- Ir a saco con el álgebra desde una perspectiva eminentemente abstracta y que los alumnos aprendan los métodos de resolución de una forma puramente metódica (que también tiene una carga de lógica y estructuración del pensamiento).
- Vemos las inecuaciones desde dónde surgieron, de la necesidad de resolver situaciones en las que las soluciones no son únicas si no que se corresponden a intervalos de la recta real.
Suelo elegir el segundo método y dedico la primera clase a resolver problemas de inecuaciones sin que conozcan las inecuaciones y que los resuelvan como a ellos les parezca mejor.
Para ello, nos dividimos en parejas o grupos y discutimos sobre los planteamientos y las soluciones. Voy dejando que sean ellos los que se planteen las preguntas y se resuelvan sus dudas.
Os comparto los dos problemas que les he planteado en este curso por si os pueden servir:
Fuente del problema: Dan Meyer
Inicio una nueva categoría del blog para mostrar curiosidades matemáticas (que algunas no lo son tanto) con el objeto de mostrar la belleza que se encierra tras las matemáticas. Os animo a descubrirla.
No existe mejor definición del sentido de las matemáticas que esta de G. H. Hardy sobre los matemáticos:
Un matemático, como un pintor o un poeta, es un creador de patrones.Si sus patrones son más permanentes que los del poeta, es porque están hechos de ideas.
Al igual que Paul Lockart en su «Lamento de un matemático» veo las matemáticas como un arte al que nadie reconoce como tal. No creo que exista algo más mágico que descubrir un patrón que se eleva por encima de la realidad que conocemos y que, sorprendentemente, el mismo patrón tiene aplicación en múltiples partes de la realidad. Un poderoso proceso de abstracción desde la realidad para volver a ella en múltiples campos. Un claro ejemplo es el álgebra, odiada por casi todos e imprescindible para todos.
Empiezo con una sorprendente regularidad numérica que involucra a todas las cifras con la participación estelar de dos números especiales, el 9 y el 11. Os animo a que descubráis el porqué de esta regularidad:


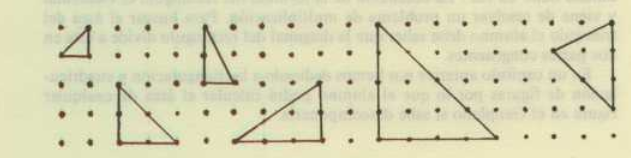
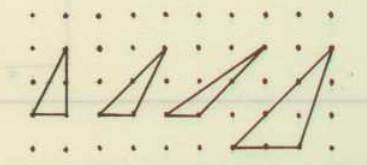













Comentarios recientes