Estos últimos cursos, he estado usando un bingo de ecuaciones de primer grado mediante una hoja de cálculo que me ha dado excelentes resultados. Durante este verano he decidido pasar muchas de estas actividades a unas webs que permiten hacer lo mismo de forma mucho más sencilla. En una entrada anterior, ya os compartí una aplicación web para hacer un bingo de conceptos de divisibilidad de forma sencilla.
Ahora he creado otra web con un bingo de ecuaciones de primer grado: «Bingo de ecuaciones de primer grado«.
En la propia web tenéis las instrucciones para llevarlo a cabo. Evidentemente no tiene ninguna dificultad.
Los pasos a seguir son los siguientes:
1. Primero elegimos el tipo de ecuaciones de primer grado que vamos a trabajar mediante los botones verdes:
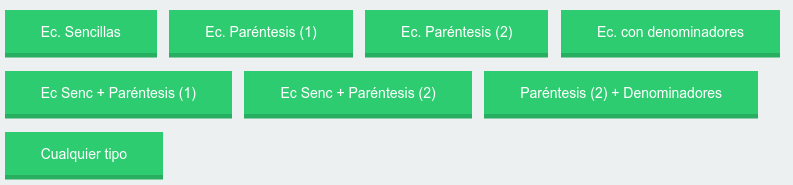
Tenemos los siguientes tipos:
- Ecuaciones Sencillas: ecuaciones que se resuelven simplemente pasando las x a un miembro y despejando.
- Ecuaciones con paréntesis (1): ecuaciones con paréntesis sencillas.
- Ecuaciones con paréntesis (2): ecuaciones con paréntesis más complejas.
- Ecuaciones con denominadores.
- «Ecuaciones sencillas + Paréntesis (1)«, «Ecuaciones sencillas + Paréntesis (2)» y «Ecuaciones con paréntesis + denominadores» : nos saldrán de forma aleatoria ecuaciones de los dos tipos.
- Cualquier tipo: nos saldrán de forma aleatoria ecuaciones de todo tipo.
Como veis hay una gran variedad de posibilidades.
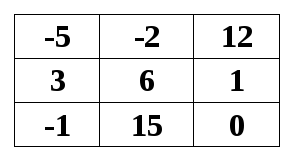
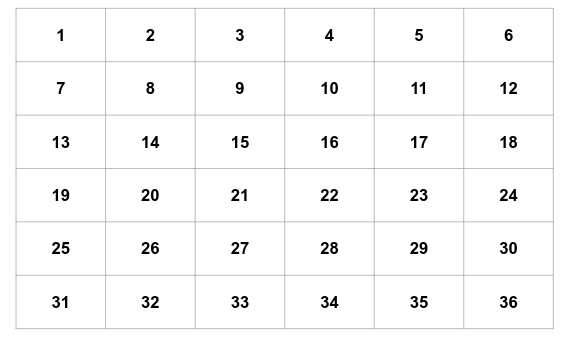
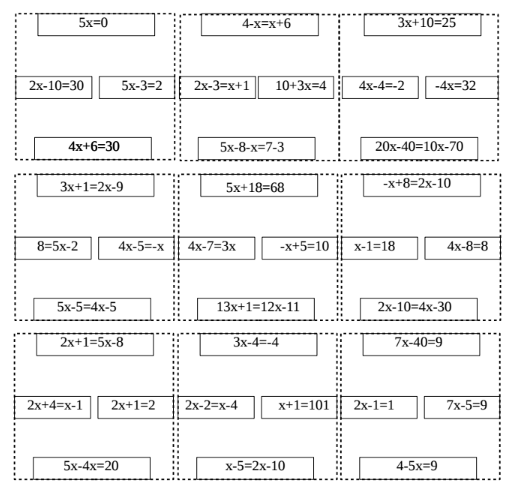
2. Los alumnos tienen que crear un cartón de bingo que consiste en una tabla 3×3. Este cartón lo tienen que completar con los números entre -5 y 15, ambos inclusive. Pueden poner los números que quieran y en la posición que deseen, lo que no pueden hacer es repetir números.
3. Una vez creados los cartones empezamos el juego en la web. Lo primero que tenemos que hacer es mostrar la primera tarjeta con el botón «Mostrar tarjeta«. Se nos mostrará una tarjeta con un enunciado (en el ejemplo, podemos leer «-2(x+1)+2(x-1)=-4(x+1)») que nos dará el primer número de nuestro bingo.

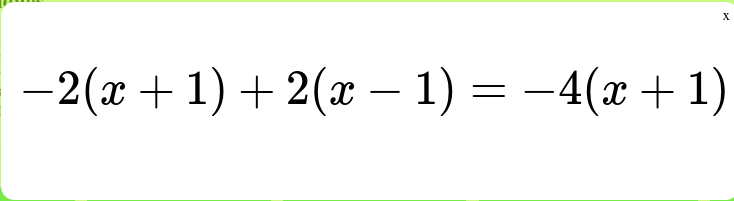
4. Para ver las tarjetas siguientes, usamos el botón «Nueva tarjeta» con lo que generamos una nueva tarjeta y luego la mostramos al igual que la primera. Seguimos el juego hasta que los alumnos canten línea y bingo.

Siempre podemos ver la solución de la tarjeta con el botón «Solución»


Durante todo el proceso del bingo, nos aparecerá un listado con las ecuaciones que hemos resuelto y sus soluciones:

5. Para empezar un nuevo bingo, basta con hacer clic en «Nuevo bingo«.
6. No os olvidéis de los premios ;-).
Otra opción
En el caso de que queráis modificar el bingo o llevarlo mediante una simple hoja de cálculo, os comparto una hoja de cálculo de Google Drive que también os puede servir.









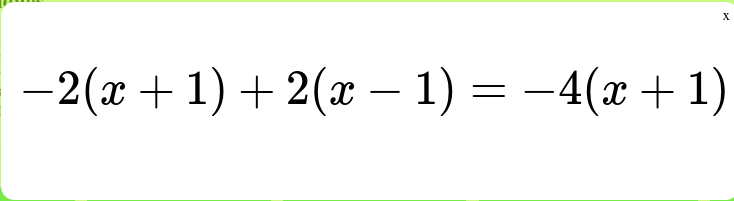





Comentarios recientes