
Happy & Sad de Farrukh
Aviso: Esta serie de entradas dedicadas a otras actividades, más motivadoras y más divertidas, que podemos realizar en el aula de matemáticas es una copia de la serie de mi blog personal.
Ante el primer día de clase, existen básicamente dos formas de enfocar esta primera sesión:
- Están los que van a saco con la asignatura y explican lo más rápido posible, las normas, los materiales, la evaluación, etc., como si no hubiera más días de clase para hablar de estas cosas. Generalmente, quieren ir rápidamente a empezar pronto con la materia ya que es el medio dónde mejor se desenvuelven (su zona de confort en el aula, que los profesores también la buscamos, tanto o más que los alumnos).
- Otros tratan de hacer la primera clase, lo que realmente es, un punto de encuentro, un momento y lugar en el que tenemos que empezar a conocernos, a saber más de nosotros y a empezar empatizar y a buscar puntos de conexión. El enfoque de la clase es totalmente distinto, nos dedicamos a lo anterior, con diferentes estrategias: diálogo sin presión, dinámicas de conocimiento, introducción a las asignatura de forma lúdica, etc.
Podemos estar en cualquiera de estos dos bandos, que cada uno elija el que quiera. Por el bien de los alumnos (del profesor) y del fluir de la clase durante el resto del curso, recomiendo encarecidamente que vayamos al segundo enfoque. Es fundamental, empezar, alumnos y profesores, con buenas sensaciones y con un clima lo más agradable posible (recuerda durante todo el curso, entrar con una sonrisa a la clase, los problemas los dejamos fuera y los que nos surjan, porque nos surgirán, los iremos solucionando con tranquilidad).
Todo lo que os he comentado anteriormente sirve para cualquier asignatura pero yo como soy de mates, os voy a hablar de la mía. Las matemáticas son una asignatura (lo que ya conlleva un rechazo a primeras del alumno, por el carácter impositivo que tienen las asignaturas) que provoca el rechazo en muchos alumnos, una asignatura estigmatizada. Sobre el porqué de esta aversión, desde hace tiempo me gustaría saber en qué momento han llegado los alumnos a ese sentimiento hacia las mates; la realidad es que a 1º de ESO llegan, muchos de los alumnos, con ese sentimiento negativo hacia la asignatura.
Además la asignatura tiene una connotación social contra la que tenemos que pelear el profesorado de matemáticas:
- Los padres y los alumnos, la consideran, a priori, una asignatura difícil con todos los prejuicios que conlleva esto. Ya comenté en este blog, en otra entrada dedicada a las matemáticas más creativas, divertidas y bellas, el comentario de una madre en el consejo escolar al decirle que era de matemáticas «¡Cómo te tienen que odiar los alumnos!». ¡Ahí queda eso, ni más ni menos! Ni me conocía, ni había preguntado a los alumnos, etc (si lo hubiera hecho se hubiera llevado una gran sorpresa ;-)). Evidentemente, se trataba de un prejuicio que puede que estuviera fundamentado en su propia experiencia, no digo que no.
- Por otro lado, está socialmente bien visto decir que soy de letras y los números no son lo mío. Recuerdo a un consejero de educación decirlo en un discurso inaugural de unas jornadas y quedarse tan ancho. Ni se las veces que he oído decir a mis compañeros con orgullo que ellos comprenden a los alumnos en su relación con las matemáticas. Jamás se me ocurrirá a mi vanagloriarme de ser una ignorante total en cualquier disciplina, me gustaría saber de todas. Sin embargo, de matemáticas se puede decir y hasta parecer que quedas bien con la gran mayoría. Pues te digo que conmigo no quedas bien, y no por no saberlo, sino por alardear de tu ignorancia. Tan perteneciente a la cultura es Cervantes como Newton o Euclides (por decir algunos).
- Y la tercera pata, es que toda la sociedad asocia la dificultad a las matemáticas. Usando una identidad tenemos «Matemáticas=díficil«. No recuerdo el banco que en su campaña de publicidad decía, más o menos, «Invertir es mucho más sencillo que hacer matemáticas». Cierto es que tienen una capa de abstracción, de razonamiento inductivo, lógico, secuencial, etc que puede generar dificultad pero de ahí a que son difíciles per se, pues no.
Pero es que las matemáticas son, y en esto subscribo la opinión de G.H. Hardy, un arte, el arte de la explicación. En este camino, hacia el desencuentro social con las matemáticas, seguramente, tenemos mucho que decir los profesores de matemáticas y los currículos que martirizan a nuestros alumnos con operaciones repetitivas, abstractas, sin sentido y, totalmente descontextualizadas que hacen formarse una idea totalmente errónea de lo que son las matemáticas, la belleza que engloban y lo fascinantes que son. El hecho de poder modelizar el mundo, simplemente con la mente humana (a lo más, con la ayuda de un lápiz y un papel), me parece sublime. Si queréis admirar la belleza de las matemáticas, os recomiendo ver estos dos vídeos de Cristóbal Vila: «Nature by numbers» e «Inspirations«. No tienen desperdicio, se los pongo mis alumnos y se les quedan los ojos como platos.
Subscribo desde la primera palabra hasta la última este párrafo sacado de «El lamento de un matemático» de Paul Lockard (que también os sugiero leer con la mente abierta y libre de prejuicios):
Si privas a los alumnos de tener la oportunidad de participar en es-
ta actividad —de proponer problemas, hacer sus propias conjeturas y
descubrimientos, de estar equivocados, de estar creativamente frustra-
dos, de tener una inspiración, y de improvisar sus propias explicaciones
y demostraciones— les estás privando de las matemáticas en sí mismas.
Así que no, no estoy protestando por la presencia de hechos y fórmulas en
las clases de matemáticas, estoy protestando por la falta de matemáticas
en las clases de matemáticas.
Si privas a los alumnos de tener la oportunidad de participar en es-
ta actividad —de proponer problemas, hacer sus propias conjeturas y
descubrimientos, de estar equivocados, de estar creativamente frustra-
dos, de tener una inspiración, y de improvisar sus propias explicaciones
y demostraciones— les estás privando de las matemáticas en sí mismas.
Así que no, no estoy protestando por la presencia de hechos y fórmulas en
las clases de matemáticas, estoy protestando por la falta de matemáticas
en las clases de matemáticas.
Si privas a los alumnos de tener la oportunidad de participar en esta actividad de proponer problemas, hacer sus propias conjeturas y descubrimientos, de estar equivocados, de estar creativamente frustrados, de tener una inspiración, y de improvisar sus propias explicaciones y demostraciones, les estás privando de las matemáticas en sí mismas. Así que no, no estoy protestando por la presencia de hechos y fórmulas en las clases de matemáticas, estoy protestando por la falta de matemáticas en las clases de matemáticas.
El lamento de un matemático de Paul Lockard.
Demoledora frase de Lockard que nos debe hacer reflexionar, tanto a los que enseñamos matemáticas como a aquellos que se dedican a decir qué tenemos que enseñar o qué tienen que aprender nuestros alumnos de matemáticas.
Y el núcleo (o igual no) de este artículo es compartir con vosotros diferentes actividades para hacer, junto a vuestros alumnos (o con vuestros hijos, ¿por qué no?), matemáticas. Unas matemáticas más cercanas, más divertidas, más abiertas y, por lo tanto, más interesantes y, no por ello, más al contrario, dejan de ser matemáticas (nos miren como nos miren). Pueden ser ideales para las primeras clases y, ¿por qué no? para trabajar durante todo el curso, las estrategias, la resolución de problemas, la deducción, etc.
Las diferentes actividades las tengo clasificadas de la siguiente forma y que tienen dedicada una entrada cada una en este blog:
En esta entrada, os voy a recomendar una batería de juegos matemáticos. Os recomiendo ver la entrada los juegos de estrategia para clase de matemáticas y que pueden complementar a los que os traigo hoy.
1. Juego de matemáticas del año 2015
Como este juego, nos podemos inventar miles de variantes sobre ka misma idea.
Con los dígitos en el año 2015 y las operaciones +, -, x, ÷, sqrt (raíz cuadrada),^ (elevar a una potencia),! (factorial), y !! (factorial doble), junto con los símbolos de agrupación, conseguir los números del 1 al 100. Las reglas son:
- Los cuatro dígitos se deben utilizar en la expresión.
- Sólo se pueden usar los dígitos 2, 0, 1 y 5. (1)
- Números de varios dígitos, como 20, 210, o 0,02 PUEDEN ser utilizados este año.Tenga en cuenta que 0,02, mientras que equivale a 0,02, no sería aceptable ya que sólo un 0 es disponible este año.
- La función cuadrado solo puede ser utilizado al usar el 2.. Tampoco se puede elevar al cubo, a la cuarta, o cualquier otra función que eleva un número a una potencia específica. Por ejemplo, (1 + 5) ^ 2 – 0! es una forma aceptable para escribir 35, porque ^ es una operación aceptable y que usa exactamente los dígitos 1, 5, 2 y 0. Pero 5 ^ 2 + 2 + 1 + 0! no es una forma aceptable para escribir 29, porque «^ 2» no es una operación aceptable, y no están disponibles dos doses. Del mismo modo, 2 ^ 3 + 5 – 1 – 0 en el electrónico no sería aceptable, ya que «^3» no es una operación aceptable.
(1) Es preferible usar el orden: 2, 0, 1, 5 .
Os dejo dos documentos que os pueden ayudar por si queréis llevarlos al aula:
2. Resolver SETS o Trifectas
Con este juego me he entretenido, y mucho, durante este verano.
El objetivo del juego es identificar un grupo SET o Trifecta de tres naipes entre doce arreglados sobre la mesa.
Un SET consiste de tres naipes en los que cada característica es igual o es diferente. Es decir, cualquier característica en el SET es común en los tres naipes o es completamente diferente. Es decir, los tres naipes en el SET deben tener el mismo color, o uno de cada color; el mismo símbolo, o uno de cada símbolo; el mismo número o uno de cada número y finalmente, el mismo tono o uno de cada tono.
Ejemplos de SETs:

Todos los tres naipes contienen el mismo símbolo, el mismo color, el mismo nombre de símbolos y todos contienen tonos diferentes.

Todos los tres naipes contienen símbolos diferentes, colores diferentes, nombres de símbolos diferentes y todos los tres tienen el mismo tono.

Todos los tres naipes contienen símbolos diferentes, colores diferentes, nombres de símbolos diferentes y tonos diferentes.
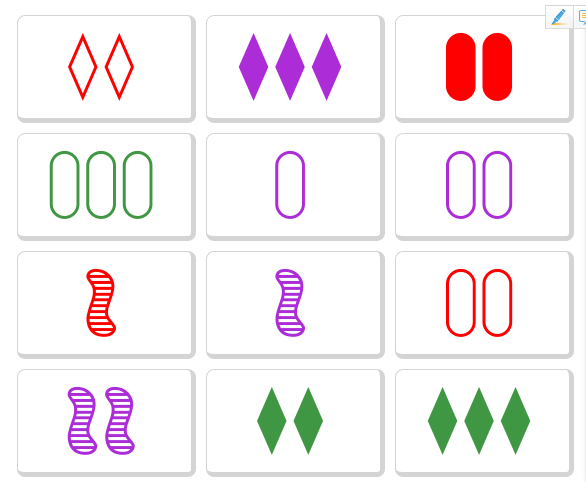
Os dejo unos cuantos tableros para que resolváis:
En este primer tablero tenéis que encontrar 4 SETs.

Encontrar 4 SETs:

Encontrar 6 SETs:
Encontrar 6 SETs:
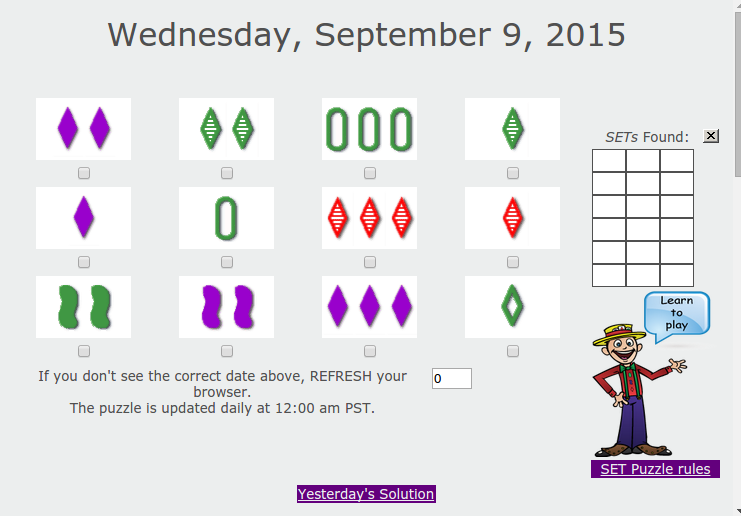
Y si queréis jugar online o recopilar más tableros de SETs o trifrectas:
3. Juego del HEX
El hex es un juego entre dos jugadores que van colocando por turnos fichas sobre un tablero romboidal, compuesto de casilleros hexagonales (generalmente de 10 por 10, 11 por 11 hexágonos, o mayores tamaños). Las fichas se distinguen por su color, asociándose uno a cada jugador, y gana quien consigue formar una línea de sus fichas que conecte dos laterales opuestos del tablero previamente asignados.
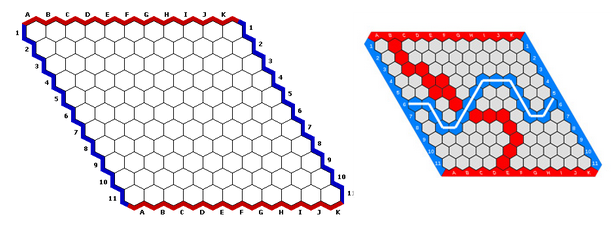
4. Juego del NIM y variantes
El Nim es un juego de mesa muy antiguo. Nim , en inglés antiguo, es “quitar” o “retirar”. Es un juego muy famoso, hasta el punto de verse reflejado en libros, como el best-seller
En este juego, dos jugadores a los que llamaremos A y B, colocan un número arbitrario de fichas (cerillas,palillos, piedras) sobre una superficie, dispuestos en varias filas. Tanto el número de filas como el número de fichas en cada fila son también arbitrarios.
El primer jugador A, toma cualquier número de fichas de un fila, entre uno y el total de la fila, pero sólo de una fila.
El otro jugador, B, hace su jugada de manera similar, retirando algunas de las fichas que quedan, y así sucesivamente, los jugadores van alternándose en sus jugadas. Gana el jugador que saca la última ficha.
Este juego se basa en la pura lógica. Por ejemplo con el juego original, que está representado debajo, el que no empieza tiene estrategia ganadora:

Os dejo otro juego Nim, muy sencillo:

Podríamos añadir muchos más juegos: sudokus, kenkens, etc. Espero que os hayan gustado y que traspaséis a vuestros alumnos el amor y la pasión por las matemáticas.
En el próximo artículo os compartiré diferentes actividades de investigación que pueden resultar, además de entretenidas y con gran contenido matemático, altamente motivantes.
Siguientes artículos de la serie:
PD: espero vuestras aportaciones con más juegos para conseguir tener una batería más potente.
El objetivo del juego es identificar
un grupo SET de tres naipes entre doce arreglados sobre la mesa.















Comentarios recientes