El Bagh Chal es un juego tradicional para dos jugadores originario del sur de Asia. Actualmente sigue siendo un popular juego en Nepal. Es un divertido juego de caza o de guerra (su característica común es la lucha entre dos fuerzas desiguales con distintos objetivos).
La expresión Bagh Chal significa, en Nepalí, algo parecido a mover los tigres.
Bagh Chal (tigres y cabras)
Se enfrentan dos bandos; uno de ellos cuenta con 4 tigres que intentan capturar a las 20 cabras del bando contrario, mientras éstas tratan de impedir moverse a los tigres.
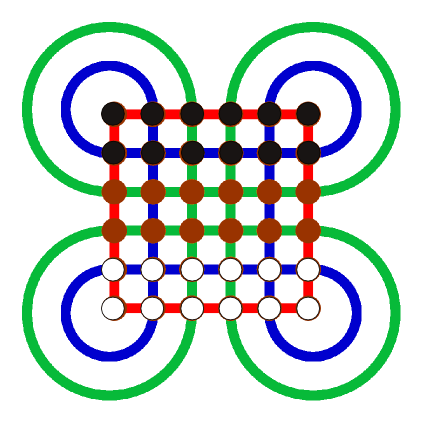
El tablero
El juego se desarrolla sobre las 25 intersecciones de un tablero cuadrado formado por 5 líneas verticales y horizontales; las intersecciones formadas entre líneas horizontales y verticales coincidentes cuyos respectivos números de orden coinciden en paridad se encuentran también unidas por líneas diagonales.

Objetivo del juego
Al ser un juego entre fuerzas desiguales, ambos bandos tienen un objetivo distinto:
- Para vencer las cabras debe cercar a los cuatro tigres de modo que ninguno de ellos pueda realizar un movimiento válido según las reglas que a continuación se explican.
- Los tigres vencen si consigue capturar cinco cabras.
Los tigres capturan a las cabras saltando por encima de ellas. No se permiten múltiples capturas.
Reglas del juego
Al iniciar el juego, las piezas se sitúan del siguiente modo: las 20 cabras se sitúan fuera del tablero y los 4 tigres en las esquinas.
Los dos jugadores realizan movimientos por turnos, comenzando el juego el bando de las cabras:
- Las cabras y los tigres pueden moverse a una intersección adyacente siguiendo las líneas.
- Los tigres capturan saltando en linea recta por encima de una cabra de la misma forma que en las damas. No es obligatorio capturar.
Lo primero que debemos hacer es colocar las cabras sobre el tablero. Para ello, se van colocando por turnos:
- En el turno de las cabras, solo pueden poner una cabra en una intersección libre.
- En el turno de los tigres, estos pueden capturar o moverse de acuerdo a las reglas.
Una vez situadas todas la cabras, no está permitido realizar ningún movimiento que produzca una situación de las piezas sobre el tablero ya repetida anteriormente.
El tablero para imprimir
Como en toda esta serie de juegos matemáticos de estrategia, os comparto un tablero para que lo imprimáis y si os parece oportuno, lo plastifiquéis. Para descargaros el tablero, hacer clic en la imagen:












Comentarios recientes