Transformamos un rectángulo de base 50 cm y altura 10 cm en un cuadrado de igual perímetro que el rectángulo. ¿En cuántos cm cuadrados se ha incrementado el área del polígono?
En línea recta, la distancia de la casa de Luisa hasta la piscina es de 5 km, y desde la casa de Nicolás a la piscina, 3 km. ¿Cuál es la distancia entre la casa de Luisa a la de Nicolás?
Se han puesto las fichas del dominó pero no se ven las líneas.
¿Puedes reconstruir las fichas?
En un torneo de baloncesto compiten 32 equipos. En cada ronda, los equipos se dividen en grupos de 4. En cada grupo, cada equipo juega exactamente una vez contra los demás. Los dos mejores equipos de cada grupo pasan a la ronda siguiente y los demás son eliminados. Después de la última ronda, los dos equipos que quedan juegan la final para determinar el ganador. ¿Cuántos partidos se han jugado en todo el torneo?
Con barras de 200g se construye una malla de 32 hexágonos dispuestos en tres filas, como se muestra en la figura.
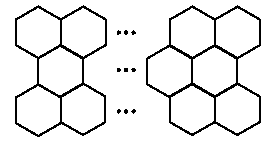
¿Cuál es la masa de la malla?
¿Cuáles son las últimas cinco cifras de la suma 1+11+111+ … + 11….111? *
* El último número tiene 2013cifras.
¿Qué ticket de descuento prefieres? ¿20 dolares (o euros) de descuento o el 20% de descuento en la compra?
Contestar razonadamente la respuesta.
Fuente: Dan Meyer
Dados los siguientes triángulos:
Qué triángulo de los anteriores cumple la siguiente descripción:El triángulo PQR es un triángulo rectángulo con el ángulo recto en R. El lado RQ es menor que el lado PR. M es el punto medio del lado PQ y N es el punto medio del lado QR. S es un punto del interior del triángulo.
El segmento MN es mayor que el segmento MS.
Nivel: Primer ciclo de Secundaria
Nota: En la solución, además del triángulo respuesta, se ha de explicar razonadamente porqué no lo son cada uno de los otros triángulos.
Hace un tiempo presenté un bingo para trabajar la factorización de identidades notables. En este bingo, se presentan identidades notables de las que hay que calcular su facturación. Por ejemplo, si aparecía x²-9, los alumnos tenía que adivinar su facturación, (x-3)(x+3).
Para trabajar de forma más completa, necesitaba un bingo que me permitiera hacer el proceso al revés (que tantas veces usamos en diferentes partes del álgebra). O sea, desarrollar aplicando las identidades notables, expresiones del tipo (x-3)², (2x+5)², … Lo podéis encontrar haciendo clic en la imagen o en la URL del final del post. Su funcionamiento es similar a todos los anteriores y los cartones para cada una de las modalidades, los podéis descargar en la misma página viendo las instrucciones.
Ya de paso, os comento que lo he puesto en funcionamiento con un curso de 2º de ESO: nos lo hemos pasado muy bien, hemos llegado a hacer todos los desarrollos a la perfección realizando alrededor de 50 desarrollos en una clase. ¡Qué alguien intente lo intente hacer sin un juego de este tipo y me cuente la reacción de los alumnos! En mi caso, todos diciendo mañana hacemos otro, pero eso es otro tema …
URL: http://www.aomatos.com/juegos/bingo-identidades-operar.php
¿De cuántas formas puede escribirse el número 100.001 como suma de dos números primos?
100.001=A+B siendo A y B primos
Nivel: Primer ciclo de Secundaria
Comentarios recientes