Quiero compartir con vosotros una serie de juegos para trabajar la divisibilidad de los números naturales de forma divertida. La gran mayoría son originales del Grupo Alquerque y fueron publicados en el nº 62 de la Revista Suma.
Los he probado durante este curso en 1º y 2º de ESO con muy buen resultado.
COLOCANDO AL DIVISOR
En este juego cada alumno juega de forma individual contra el resto de sus compañeros.
Tienen que dibujar en su cuaderno un tablero como el siguiente:

El profesor lanza un dado cúbico nueve veces. Los alumnos deben anotar los resultados que van saliendo en las nueve celdas del tablero. Una vez completo, se anotan a la derecha y debajo las puntuaciones. Se anotan un punto por cada divisor que hemos colocado del número que hay a la izquierda de la fila. Por ejemplo, si en la primera fila (nº 24) hemos puesto el 4, 5, 6, anotaríamos dos puntos a la derecha ya que 4 y 6 son divisores de 24. De igual forma anotaríamos los puntos por columnas. La suma de todas la puntuaciones nos da el total. Gana el alumno que consigue la máxima puntuación.
Siguiendo las recomendaciones de la publicación mencionada anteriormente, hice tres pases diferenciados:
- Primero jugaron sin saber las reglas.
- Repetimos la partida conociendo ya las reglas.
- Hacemos una tercera partida anotando los resultados y colocándolos en el tablero una vez que han salido los nueve.
- Hacemos una última tirada pero ganando el que menos puntuación saca.
Debemos animar a los alumnos a deducir la mejor estrategia y que se la expliquen a los demás. En mi caso, Salma, la dedujo con precisión y se la explicó perfectamente a sus compañeros.
BÚSQUEDA DE DIVISORES
Juego para dos jugadores.
Se crean un tablero con los números del 1 al 45:

El modo de jugar es el siguiente:
- El jugador A tacha un número sobre el tablero y lo anota en su tabla de puntuación.
- El jugador B tacha todos los divisores del número tachado por el compañero que estén sobre el tablero y va anotando esos números en su tabla de puntuación. Una vez terminado tacha cualquier otro número no tachado del tablero y lo anota en su tabla.
- Se invierte el turno; ahora el otro jugador (el A en este caso) repite el paso 2.
- Se van alternando los turnos hasta que no quede ningún número sin tachar sobre el tablero.
- Si un jugador olvida tachar un divisor y su contrincante se da cuenta, el contrario puede tacharlo y anotarlo en su cuenta aunque no sea su turno.
- Gana el jugador que sume más puntos en su tabla de puntuación.
LABERINTO DE MÚLTIPLOS Y DIVISORES
Dado el siguiente tablero:

Encontrar caminos que entren por alguno de los extremos de la izquierda y salgan por alguno de la derecha, con la condición de qe podemos pasar de una celda a otra que la toque siempre y cuando sean múltiplos o divisores entre si.
Podemos ver que pueden hacerse cuatro recorridos distintos por lo menos. Les podemos animar a encontrar el más corto y el más largo para cada entrada y salida.
JUEGO DE LOS NÚMEROS PRIMOS
Juego de parejas con el siguiente tablero:

Reglas del juego:
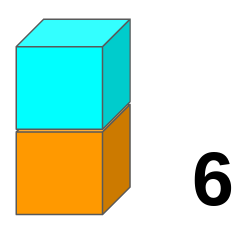
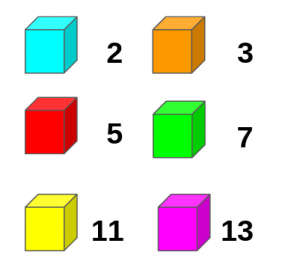
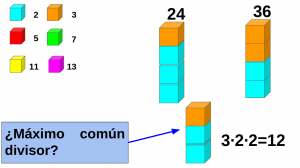
- Un jugador, en su turno, lanza dos veces el dado y compone un número de dos cifras en el orden en que han salido los números, por ejemplo el 36. Coloca una ficha sobre un divisor de ese número, por ejemplo el 2, en su propio tablero. Se queda con el cociente de la división 36:2 = 18 y vuelve a repetir el proceso con el 18. Por ejemplo coloca una ficha sobre un 3 y se queda con el valor 18:3 = 6. Continua hasta que no encuentre más divisores y en ese caso pasa el turno al otro jugador.
- Si el número inicial que construye es primo, no está sobre el tablero y el jugador lo descubre tirará de nuevo, pero si no lo hace pasa el turno al otro jugador. Si el jugador dice que el número es primo, pero no lo es, el otro jugador puede poner en su tablero las fichas de los divisores que descubra y a continuación coger el turno.
- Gana quien primero llene una fila y una columna.
MULTIPLICADORES Y DIVISORES HASTA 36
Este juego no pertenece a la publicación antes mencionada y que encontré por Internet hace mucho tiempo y no recuerdo dónde. Este juego es muy divertido y tienen que tratar de buscar estrategias ganadoras.
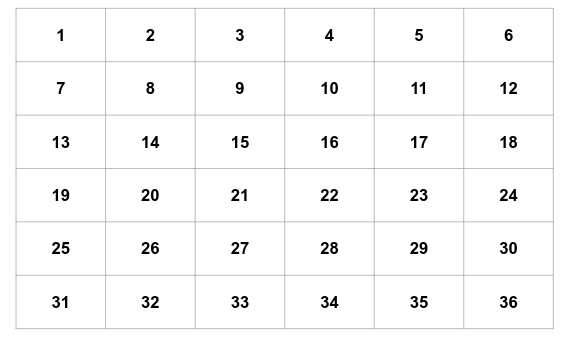
Nos creamos un tablero con los 36 primeros números:

Reglas del juego:
Se juegan dos jugadores. Empieza un jugador por un número par que debe tapar del tablero. En la jugada siguiente, el otro jugador debe tapar un múltiplo o divisor del elegido por el contrincantes. Se siguen las jugadas con las mismas condiciones hasta que un jugador no puede colocar ningún número. Dicho jugador habrá perdido el juego.
Podemos complicar el juego poniendo un tablero con más números.
Espero que os hayan gustado.









Comentarios recientes