Este es un post que complementará un artículo, que espero publicar en breve, en el que mostraré el método que uso para empezar a resolver las ecuaciones de primer grado de forma manipulativa y que a los alumnos les encanta.
Me gusta mostrarles las ecuaciones como una balanza de pesas en las que alguna de ellas es desconocida con el objetivo de adivinar el peso de dicha pesa.

Para ello podemos añadir o quitar pesas pero siempre con la condición de que la balanza quede equilibrada. No les es complicado deducir el procedimiento a seguir: añadir o quitar el mismo número de pesas iguales en ambos lados, hacer los mismos trozos en pesas de ambos lados (despejar), … con el objetivo de dejar la pesa (la x) sola en un plato obteniendo en el otro plato la respuesta.
Veamos dos ejemplos que nos ayudarán a entender mejor el proceso de diferentes formas y con diferentes dificultades:
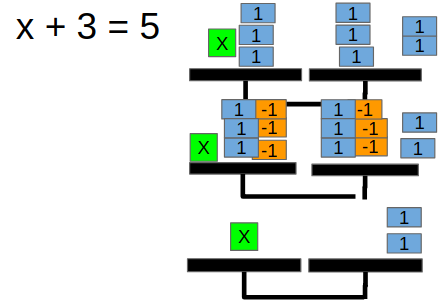
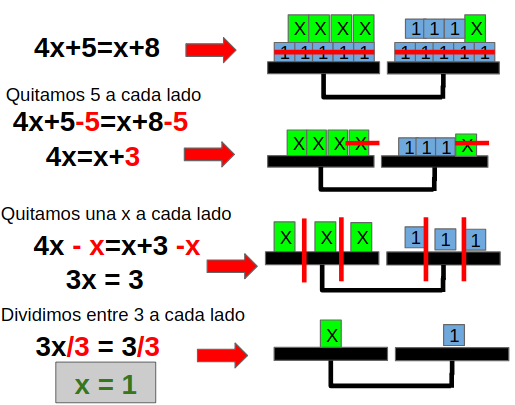
Aunque ahora uso un método manipulativo, me gusta mucho que practiquen y experimenten la resolución mediante programas interactivos.
En los últimos años, he usado las aplicaciones de la Biblioteca Nacional de Manipuladores Virtuales (NLVM) de la Universidad de Utah. Dichas aplicaciones están realizadas en Java y ahora es muy complicado hacerlas funcionar en los centros o en los ordenadores de los alumnos. Lo mismo me ha sucedido con las aplicaciones del Instituto Freudenthal. En un post que escribí hace unos años, podéis tratar de hacer funcionar dichas aplicaciones y veréis el problema del que os hablo.
Afortunadamente he encontrado otros excelentes interactivos que me permiten suplir los anteriores de forma bastante digna y son los que os quiero mostrar en este artículo.
Balanza de naturales del NVLM
Empiezo por el más simple que está basado en una de las balanzas del NLVM y que se queda un poco corto. Nos puede servir para practicar ecuaciones con números naturales. No necesita mucha explicación: se iguala la balanza con los objetos, pulsamos en continuar y vamos realizando las operaciones hasta llegar al resultado.
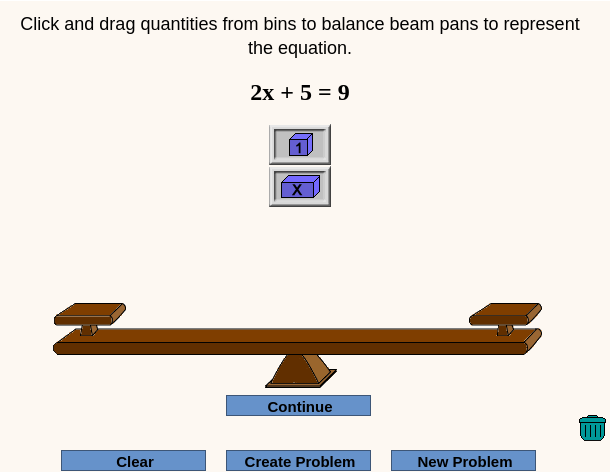
URL: http://www.hoodamath.com/mobile/games/algebra-balance-equations/game.html
Equality Explorer del PHET
En la biblioteca de «Simulaciones Interactivas» de la Universidad de Colorado podemos encontrar una joya para trabajar este tema desde los niveles más elementales y de forma muy interactiva.
El interactivo nos lo podemos descargar para trabajar offline, lo tenemos en diferentes idiomas y con unas propuestas para llevar al aula:

El interactivo tiene diferentes niveles.
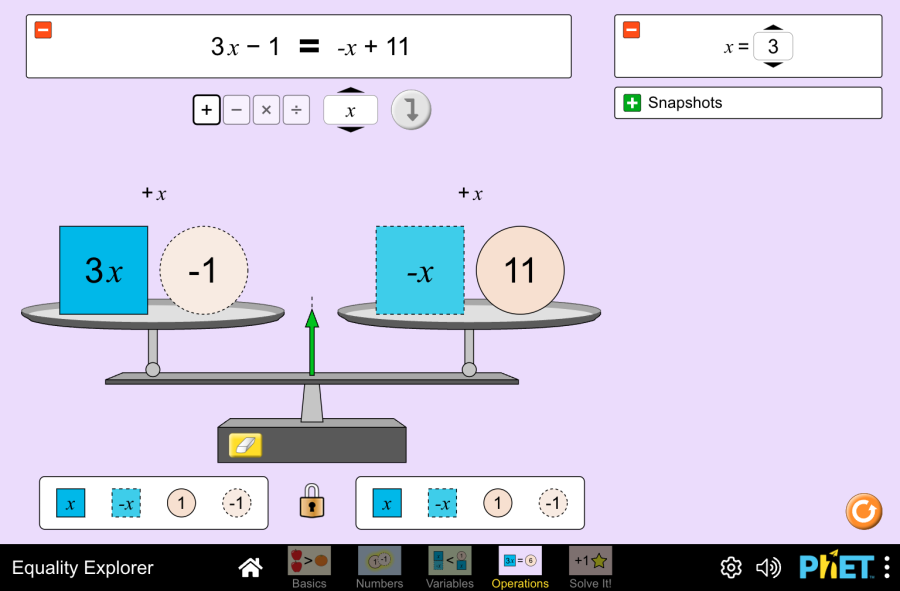
Os recomiendo usar los siguientes:
- Empezar con el básico para que se acostumbren a manejar las balanzas y que resuelvan los diferentes problemas que podemos encontrar: peso de los objetos, peso relacionado de frutas, monedas, etc.
- Operaciones para construir sus propias ecuaciones y practicar la resolución con la balanza y jugar con la comprobación de las soluciones.
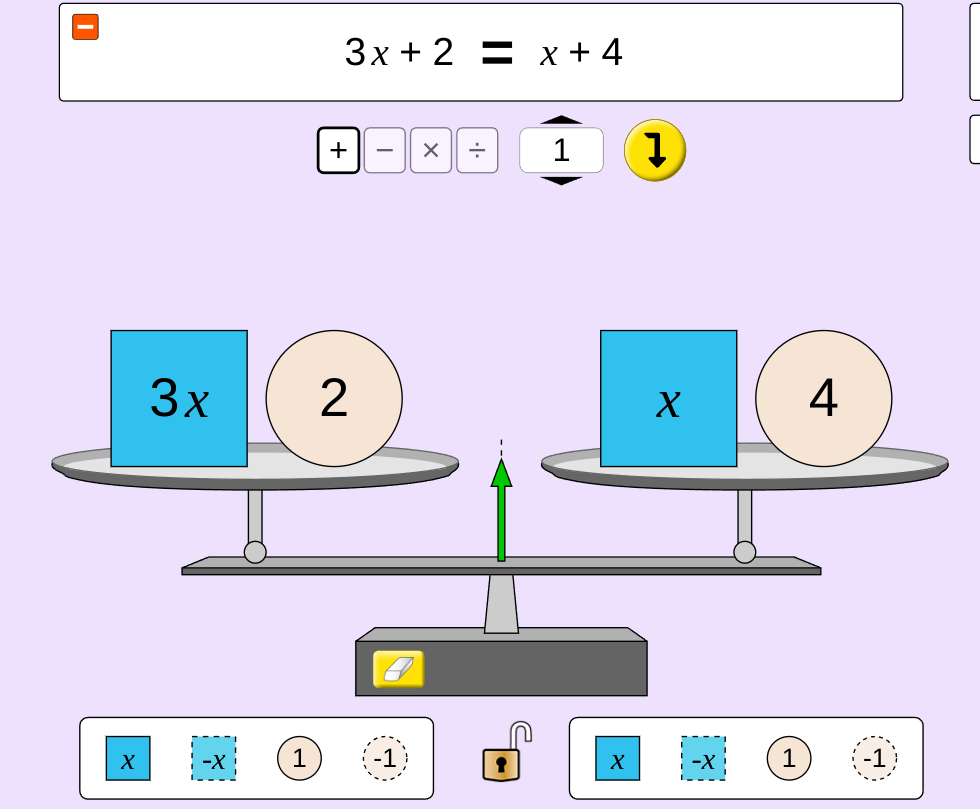
- Resuélvelo en el que tenemos diferentes ecuaciones con diferente nivel de dificultad para resolver.
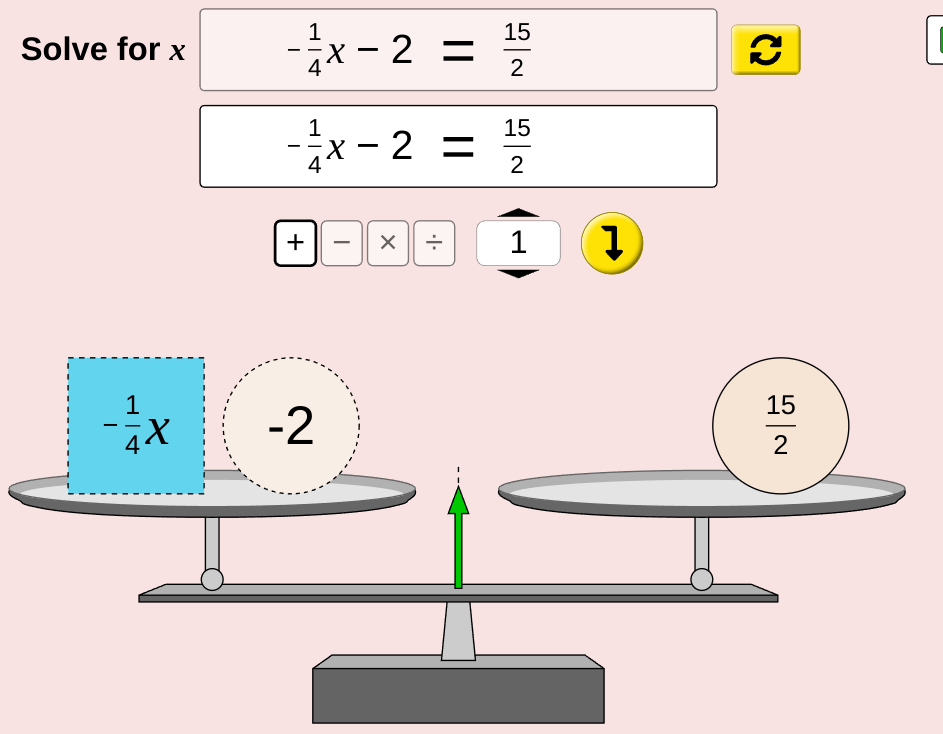
Libro de Geogebra con balanzas algebraicas
En el siguiente libro de Geogebra, tenéis dos balanzas algebraicas para aprender poco a poco el método de resolución de ecuaciones mediante balanzas algebraicas.
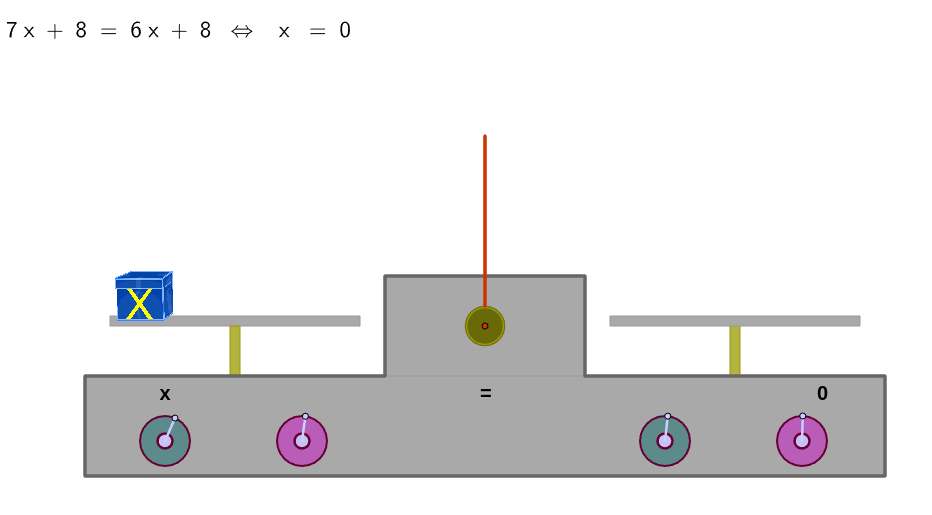
Espero que os gusten y les podáis sacar provecho con vuestros alumnos o hijos.
Continuación…
Si queréis seguir trabajando este tema de forma divertida con vuestros alumnos os recomiendo leer los siguientes posts:












Comentarios recientes