Ana trazó segmentos uniendo todos los puntos de la parte de arriba con todos los puntos de la de abajo. ¿Cuántos segmentos trazó Ana?
Tenemos nueve monedas que son iguales a simple vista, pero sabemos que una es falsa. La moneda falsa pesa un poco menos que las verdaderas. Para averiguar cuál es la falsa tenemoa una y sólo podemos utilizarla dos veces. ¿Cómo encontrarías la moneda falsa?
Algunos números de tres cifras tiene esta propiedad: si les quitas la primera cifra queda un cuadrado perfecto y si le quitas la última, también queda un cuadrado perfecto. ¿Cuánto vale la suma de todos estos números con tan curiosa propiedad?
Transformamos un rectángulo de base 50 cm y altura 10 cm en un cuadrado de igual perímetro que el rectángulo. ¿En cuántos cm cuadrados se ha incrementado el área del polígono?
En línea recta, la distancia de la casa de Luisa hasta la piscina es de 5 km, y desde la casa de Nicolás a la piscina, 3 km. ¿Cuál es la distancia entre la casa de Luisa a la de Nicolás?
En un torneo de baloncesto compiten 32 equipos. En cada ronda, los equipos se dividen en grupos de 4. En cada grupo, cada equipo juega exactamente una vez contra los demás. Los dos mejores equipos de cada grupo pasan a la ronda siguiente y los demás son eliminados. Después de la última ronda, los dos equipos que quedan juegan la final para determinar el ganador. ¿Cuántos partidos se han jugado en todo el torneo?
Con barras de 200g se construye una malla de 32 hexágonos dispuestos en tres filas, como se muestra en la figura.
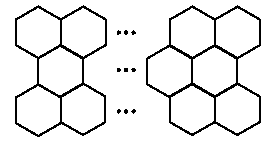
¿Cuál es la masa de la malla?
¿Cuáles son las últimas cinco cifras de la suma 1+11+111+ … + 11….111? *
* El último número tiene 2013cifras.
Se han puesto las fichas del dominó pero no se ven las líneas.
¿Puedes reconstruir las fichas?
Comentarios recientes