Vamos con otro examen más de la serie de Oposiciones. En este caso vamos a ver el examen de Madrid de 2023 de la convocatoria de estabilización. Parece ser que en 2023 hubo dos oposiciones, una de estabilización y la otra, de acceso libre. El examen de esta convocatoria, como veréis a continuación es bastante más sencillo que el de la convocatoria de acceso libre y, sin lugar a dudas, el más simple que he visto nunca en una oposición.
El examen lo podéis encontrar en este enlace: Estabilización Madrid 2023
Veámoslo ejercicio por ejercicio.
Ejercicio 1
Un ejercicio de análisis que tuve que leer varias veces ya que no daba crédito a su sencillez.
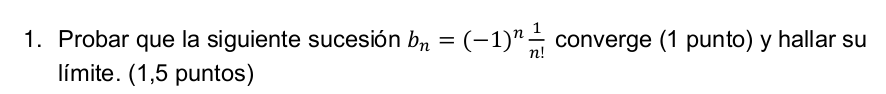
Solución: Madrid-2023-estabilizacion-solucion-ejer1
Ejercicio 2
Un ejercicio de geometría en polares que no tiene mayor dificultad. En el apartado 4, se pide hallar una longitud de arco que sale muy sencilla en polares pero si alguien no se acuerda de cómo se hacía en polares, es sencillo hacer una parametrización y hacerlo en paramétricas.

Solución: Madrid-2023-estabilizacion-solucion-ejer2
Ejercicio 3
Un ejercicio de probabilidad de un nivel de 2º de bachillerato o incluso de 4º de ESO si se han visto árboles de probabilidad.

Solución: Madrid-2023-estabilizacion-solucion-ejer3
Ejercicio 4
Un típico ejercicio de álgebra lineal con cambios de base y una función lineal. Sabiendo lo justo de las ecuaciones de cambios de base se realiza en muy poco tiempo.
















El enlace a la solución del problema 2 de Navarra 2021 (Castellano) no funciona.
Por otro lado, en el 3, donde pone la gamma de 1/3, entiendo que es para sacar la solución numérica aunque en el examen se dejaría indicado ¿no?
Saludos, felicidades por la página que está fenomenal.
Hola Carlos,
Efectivamente, se me ha olvidado poner el enlace. En breve lo soluciono.
Sobre la función gamma, es posible que con indicarlo sea suficiente, no lo sé.
Gracias por tus palabras.
Si te ha gustado el blog mira mi web sobre «Ideas y recursos educativos para matemáticas»: https://aomatos.com/recursosmates/.
Un saludo.