Aplicaciones para operar con matrices

26. junio 2025 · 2 comentarios · Categorías:Álgebra, Bachillerato, Interactivos Geogebra, Manipulables · Etiquetas:, ,

Retomo el blog tras un tiempo parado para ir poco a poco haciendo entradas de recopilaciones de los materiales interesante que voy encontrando en la red.

Empiezo hoy con unas aplicaciones para realizar operaciones con matrices.

Matrix Multiplication

Una herramienta muy sencilla y muy visual para realizar multiplicaciones de matrices: Matrix Multiplication

En el siguiente vídeo podéis ver su funcionamiento:

Matrix Calculator

Matrix calculator es una excelente aplicación en la que podemos hacer todo tipo de operaciones de álgebra matricial. En la siguiente imagen vemos lo que podemos hacer con matrices:

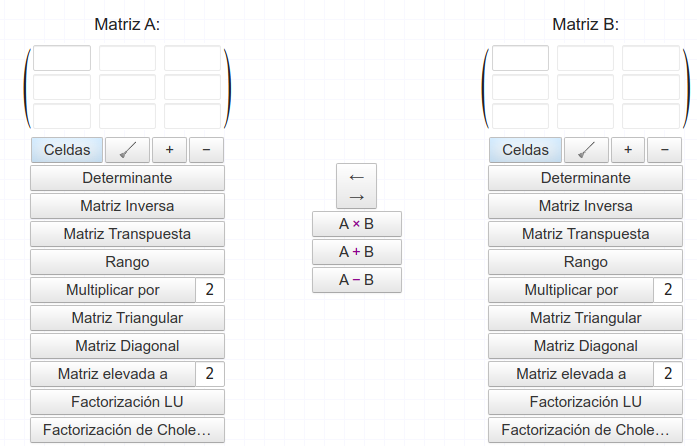
Las principales opciones que tenemos son:

  1. Operaciones con matrices: hallar el determinante, la inversa, la traspuesta, hallar el rango, cualquier potencia, triangularla, diagonalizarla, …
  2. Resolver sistemas de ecuaciones: resolver sistemas por Gauss, por la inversa, por el método de Cramer, …
  3. Calculadora de determinantes:  nos ayuda a encontrar el determinante, ampliando una fila o columna, utilizando la fila de reducción para obtener ceros en una fila o columna. Y lo bueno es que podemos ver los resultados intermedios.
  4. Calculo de los valores y vectores propios

Matriz Inversa

Este recurso no tiene ni mucho menos el nivel de los anteriores pero os lo comparto de igual manera.

Es un sencillo Geogebra creado por mi para practicar el cálculo de la inversa de matrices 2×2 y 3×3.

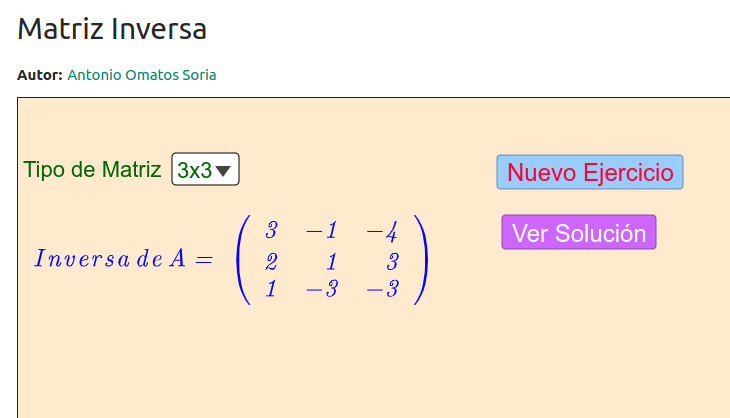
Eso es todo, espero que os gusten.

Recursos e ideas para la clase de matemáticas

26. junio 2025 · 5 comentarios · Categorías:Recursos · Etiquetas:,

En febrero y marzo del curso 2017/2018, impartí en el «CIFE de Logroño» un curso titulado como esta entrada «Recursos e ideas para la clase de matemáticas«.

El objetivo que figuraba en la convocatoria era  «dar al profesorado estrategias y recursos motivantes que  justifiquen la necesidad de conocer las matemáticas a través de proyectos de investigación, tecnologías que mejoren el aprendizaje y la resolución de problemas como reto formativo de primer orden. Todo ello desde mi perspectiva de uso en el aula, viendo aquellas herramientas que a mi me sirven, aquellos proyectos que me han funcionado (y también aquellos que no), usando recursos sencillos que resultan motivadores para el alumnado, etc,»

Sin entrar en más profundidades, me gusta entender las matemáticas en base a estas palabras de G. H. Hardy:

Un matemático, como un pintor o un poeta, es un creador de patrones. Si sus patrones son más permanentes que los del poeta, es porque están hechos de ideas.

Y si a las palabras de Hardy le añadimos las de Goethe “Saber no es suficiente, debemos aplicar. Desear no es suficiente, debemos hacer”, se nos presenta el aula de matemáticas como una bella excusa para pensar como decía el amigo “Ángel Ramírez”:

El curso constaba de cuatro ejes fundamentales que coincidían con las diferentes sesiones, excepto el primero que constaba de dos sesiones:

  • Utilidades y recursos TIC: Desmos, Kahoot, Plickers,ThatQuiz, libros de GeoGebra … (dos sesiones)
  • Proyectos matemáticos: restaurante matemático y otros guisos
  • Juegos matemáticos para el aula: puzzles, bingos, cuatro en raya
  • Ideas y recursos varios para el aula: cine y matemáticas, matemáticas en tres actos, investigaciones matemáticas.

En la siguiente presentación, que fue la introducción al curso podéis haceros una idea de parte del curso:

Sin embargo, mi objetivo era mucho menos ambicioso. Trataba fundamentalmente de compartir con mis compañeros mi visión de la educación matemática y, fundamentalmente, compartir los recursos que he ido creando estos años para el aula.

Por este mismo motivo, y tras darle muchas vueltas debido a la exposición que esto supone, he decidido compartir con todos vosotros la web que creé para recoger todos los materiales que compartí durante el curso. Una web que independientemente de que estemos de acuerdo en el enfoque didáctico, tiene muuuucho trabajo detrás. Espero que os guste y que podáis sacar provecho de los múltiples materiales que hay en ella.

No os entretengo más y os dejo el enlace de la web:

Ideas y Recursos para la clase de matemáticas

Examen oposiciones La Rioja 2025 (3)

25. junio 2025 · Escribe un comentario · Categorías:Oposiciones · Etiquetas:

En anteriores entradas, publiqué los dos primeros ejercicios con su solución:

Veamos el tercero.

Ejercicio 3

Sean dos circunferencias de radios R y r, con centros, respectivamente, O y O’ que son tangentes exteriores en el punto A.

Por el punto A se traza la recta tangente común a ambas circunferencias.

Si desde un punto cualquiera, B, de dicha tangente, se trazan dos rectas tangentes, una a cada una de las circunferencias, los puntos C y C’ son, respectivamente, son los puntos de tangencia.

  1. Hallar el límite del cociente de las áreas de los triángulos ABC y ABC’  cuando B se aproxima a A.
  2. Hallar el límite del cociente de las áreas de los triángulos ABC y ABC’ cuando B se aleja indefinidamente de A.

La clave de este ejercicio es darse cuenta que los segmentos BC y BA son iguales. Luego se ve que los triángulos OAB y ADB son semejantes lo que nos permite poner el área del triángulo ADB (que es la mitad del ABC) en función de R y b (distancia de A a B). Luego basta con hallar los límites cuando b (distancia de A a B) tiende a cero y cuando b tiende a infinito.

En el siguiente geogebra se puede ver con claridad:

Os adjunto un documento con todo el ejercicio resuelto: ejer03-larioja-2025

Examen oposiciones La Rioja 2025 (2)

25. junio 2025 · Escribe un comentario · Categorías:Oposiciones · Etiquetas:

En la anterior entrada, publiqué el primer ejercicio con su solución. Ahora vamos a por el segundo.

Ejercicio 2

  1. Las raíces de la ecuación x^3-16x^2+81x-128=0 son las longitudes de los lados de un triángulo. Encuentra el área del triángulo.
  2. Resolver la integral: \displaystyle \int\frac{\sqrt[3]{1+\sqrt[4]{x}}}{\sqrt{x}}\, dx

Las ideas para la resolución son las siguientes:

  1. Usar la fórmula de Herón (A=\sqrt{s(s-a)(s-b)(s-c)} , s el semiperímetro) junto a las ecuaciones de Cardano- Vieta.
  2. Aplicar cambios de variable para eliminar las raíces y llegar a una expresión polinómica.

Os adjunto un documento con todo el ejercicio resuelto: ejer02-larioja-2025

Examen oposiciones La Rioja 2025 (1)

24. junio 2025 · Escribe un comentario · Categorías:Oposiciones · Etiquetas:

El sábado, 21 de junio de 2025, se realizaron los exámenes de las oposiciones de La Rioja de Profesores de Secundaria de Matemáticas. A día de hoy, martes 11 de junio, no han publicado la prueba de la fase práctica ( los que llamamos los problemas) pero por diferentes fuentes he conseguido tres ejercicios de los cuatro que conforman la prueba. Es curioso que no hayan publicado el examen de matemáticas ya que en otras especialidades sí que estaban publicados. También sé que no les dejaron sacar el examen. Sinceramente, desconozco el motivo. Seguiremos esperando.

Os adjunto un pdf con las tres preguntas con las cuatro preguntas  que tengo y en  caso de obtener la cuarta la publicaré en el mismo documento: LaRioja-2025

En esta entrada, voy a analizar y dar el resultado de uno de ellos. En siguientes entradas resolveré el resto de ejercicios.

Ejercicio 1

Dada la siguiente función: f(x)=\begin{cases}0\text{ si } x\leq 0 \\kxe^{-x^2}\text{ si } x>0\end{cases} se pide:
  1. Hallar el valor de k para que f(x) sea la función de densidad de una variable aleatoria continua X.
  2.  Calcula la función de distribución.
  3.  Calcula moda y mediana.
  4.  Calcula media y varianza.

Un ejercicio de distribuciones de probabilidad, a priori, bastante asequible  aunque en el desarrollo del ejercicio nos vamos a encontrar con integrales de la función gamma que pueden imposibilitar su resolución.

Antes de adjuntar la solución os comento lo que hay que saber en cada apartado para resolver el problema:

  1. Para que f sea función de densidad se ha de cumplir que el área comprendida entre f y el eje X ha de ser 1 que será la probabilidad total. Recordemos que en una variable aleatoria continua, la probabilidad P(X\leq x) viene dada por \int_{-\infty}^{x}f(x)dx. Por lo tanto,  hemos de hallar k para que \int_{-\infty}^{\infty}f(x)dx=1. La integral es muy sencilla por lo que no hay mayor problema para resolverlo.
  2. La función de  distribución es F(x)= P(X\leq x)=\int_{-\infty}^{x}f(x)dx.
  3. La moda es el máximo de la función de densidad. Evidentemente solo puede existir para valores positivos. Simplemente derivar y halla el valor máximo de f. La mediana es el valor que ocupa la posición central, por lo tanto es el valor que F(x_0)= P(X\leq x_0)=0,5.
  4. La media es \mu=\int_{-\infty}^{\infty}xf(x)dx y la varianza \sigma^2=\int_{-\infty}^{\infty}(x-\mu)^2f(x)dx. 

Os adjunto un documento con todo el ejercicio resuelto: ejer01-larioja-2025