Saltar la navegación

NRICH y otras hierbas

NRICH

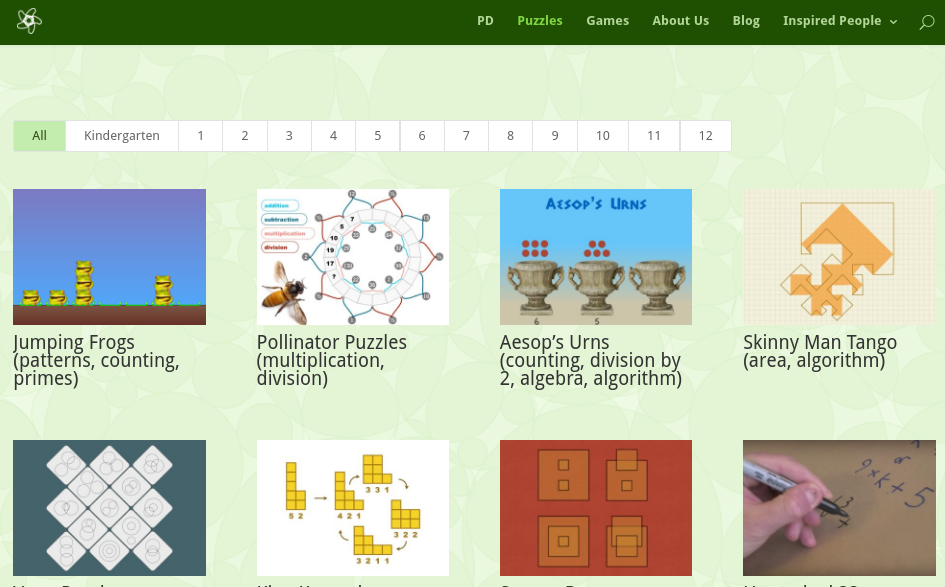
El proyecto NRICH  de la Universidad de Cambridge, pretende enriquecer las experiencias matemáticas de todos los estudiantes. Para apoyar este objetivo, los miembros del equipo NRICH trabajan en una amplia gama de capacidades, incluyendo el desarrollo profesional para profesores que desean incorporar tareas ricas de matemáticas en la práctica cotidiana de la clase.

Es uan web imprescindible si queremos trabajar con tareas ricas o abiertas.

Debido a la gran cantidad de material que podemos encontrar en NRICH, que bien merece la pena bucear por su contenido, he creado una presentación con una recopilación por nivel de dificultad de las tareas más interesante que he encontrado:

Más información en el siguiente artículo: https://revistasuma.es/IMG/pdf/72/099-103.pdf

Mathpickle

Otra excelente web llena de juegos y puzzles.

Blog de Don Steward

Un blog lleno de recursos y de ideas para las clases de matemáticas. Debido a los excelentes y abundantes materiales que publica, tengo creadas presentaciones que van recopilando sus mejores recursos:

 URL: http://donsteward.blogspot.com

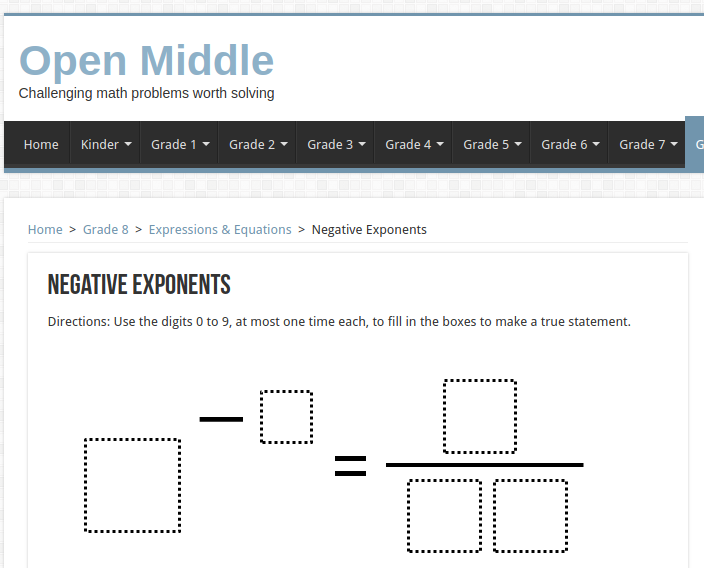
OpenMiddle

Web dedicada a recopilar actividades "Open Middle" (muy similares a las tareas ricas o abiertas). 

En la propia web las definen como:

  • tienen un "comienzo cerrado", lo que significa que todos comienzan con el mismo problema inicial.
  • tienen un "final cerrado" lo que significa que todos terminan con la misma respuesta.
  • tienen un "medio abierto", lo que significa que hay múltiples maneras de abordar y finalmente resolver el problema.

Algunas características adicionales de problemas "Open Middle"  incluyen:

  • A menudo tienen múltiples formas de resolverlos en lugar de ser un problema donde se les dice que lo resuelvan usando un método específico.
  • Pueden implicar la optimización, de tal manera que es fácil obtener una respuesta, pero es más difícil obtener la mejor respuesta u óptima.
  • Pueden parecer de naturaleza simple, pero resultan ser más desafiantes y complejos cuando comienzas a resolverlo. 
  • Por lo general, no son tan complejas como una tarea de rendimiento que puede requerir un contexto de contexto significativo para completarse.

URL: http://www.openmiddle.com  

WHICH ONE DOESN'T BELONG?

Web basada en el libro "Which One Doesn't Belong?" en el que se nos presentan cuatro imágenes relacionadas en las que tenemos que argumentar cuál de ellas no pertenece al grupo que forman las demás.

Se nos plantean múltiples tareas abiertas ya que en la gran mayoría de los casos podemos desechar más de una imagen cambiando la definición del grupo que forman las demás. 

Por ejemplo, si elegimos la siguiente imagen, podemos argumentar para que las cuatro gráficas sean las diferentes:

- La primera imagen es una función par (simétrica respecto al eje Y).

- La segunda imagen es la única que no corta al eje X.

- La tercera imagen es la única parábola con las ramas hacia arriba ( el coeficiente de x² es positivo).

- La cuarta imagen es la única imagen con un único punto de corte con el eje X.

Como vemos nos aporta un excelente método para debatir en clase y lo que es más importante, obligar a los alumnos a verbalizar sus ideas con rigor matemático. Este último aspecto es una de las cosas que más les cuesta hacer. Saben hacer las cosas pero les cuesta mucho explicar cómo lo hacen.

Podemos encontrar cuatro categorías de imágenes:

  • Figuras
  • Gráficos
  • Números
  • Conjuntos incompletos. Ideal para que los alumnos piensen qué pondrían en las imágenes que faltan.

URL: http://wodb.ca/

Puntmat

PuntMat es un espacio de información y divulgación de actividades, materiales y reflexiones entorno a la enseñanza de las Matemáticas en la etapa obligatoria. Quiere ser una herramienta útil al servicio de los docentes a la hora de preparar su trabajo. 

URL:  http://puntmat.blogspot.com 

Estimation 180º

Web creada por Andrew Stadel, en la que encontramos una colección de desafíos para trabajar la estimación dentro de las matemáticas. 

Para que os hagáis una idea, os pongo uno de los desafíos:

"Cuántos cheetos caben en el plato?

La gran mayoría de los desafíos se pueden adaptar al método de los 3-act de Dan Meyer.

URL: http://www.estimation180.com/

Visual Patterns

Web que recoge una excelente colección fotos de series con patrones numéricos. Ideales para trabajar las sucesiones o series de una forma más visual y lúdica.

Ejemplos:

 

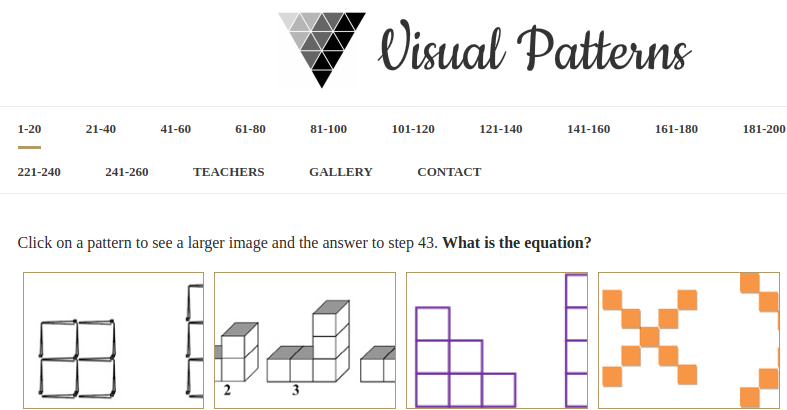
URL: http://www.visualpatterns.org/

Brilliant

URL: https://brilliant.org