Teoría

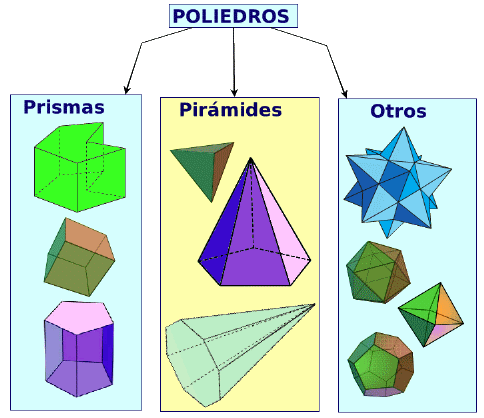
 POLIEDROS

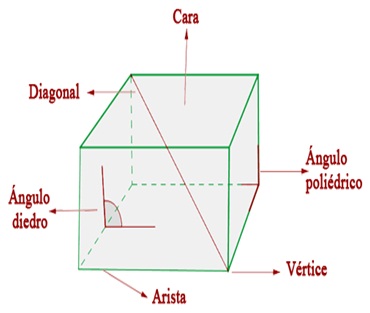
• Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos, siendo cada uno de ellos una cara.
• Se llaman caras del poliedro a los polígonos que lo limitan.
• Se llaman aristas del poliedro a los lados de los polígonos que lo limitan.
• Se llaman vértices del poliedro a los vértices de los polígonos que lo limitan.

 

Los poliedros en la Vida Cotidiana

En nuestro entorno encontramos diversos objetos con formas poliédricas.Los balones de fútbol han estado hechos siempre con 12 pentágonos y 20 hexágonos (icosaedro truncado), aunque hoy día algunos han cambiado por otra forma poliédrica más redondeada (el pequeño rombicosidodecaedro) que tiene 20 triángulos, 30 cuadrados y 12 pentágonos.

 

En sus formas naturales, muchos minerales cristalizan formando poliedros característicos.

 

 

 

 En 1996 se concedió el premio Nobel de Química a tres investigadores por el descubrimiento del fullereno (C60), cuya forma es un icosaedro truncado. 

Los panales de abejas tienen forma de prismas hexagonales.

 

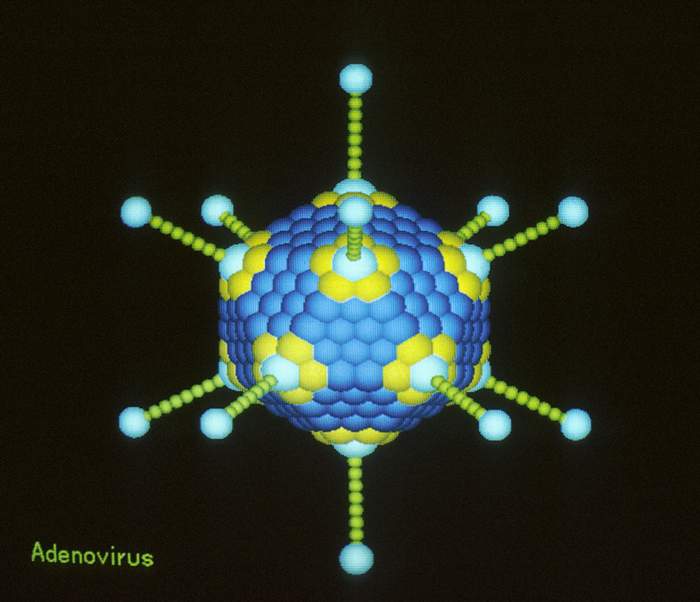
Los virus de la poliomelitis y de la verruga tienen forma de Icosaedro. Las células del tejido epitelial tienen forma de cubos y prismas.

 

 En pintura, Salvador Dalí utiliza el dodecaedro en un óleo para enmarcar su escena sobre la última cena (con sus 12 Apóstoles). También lo utiliza en su obra Crucifixión (la cruz se compone de 8 hexaedros adosados).

 

Actividad

Captura todas las imágenes que veas en la vida real en la que estén representados  poliedros.

Clasificación de los poliedros

Según la forma de los ángulos diédricos

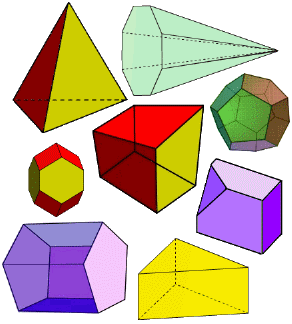
• Un poliedro se llama convexo si todo él está en el mismo semiespacio respecto al plano de cada una de sus caras, es decir, al prolongar cualquiera de sus caras, éstas no cortan al poliedro.
• Poliedro cóncavo es el que tiene alguna cara cuyo plano atraviesa a la figura, o sea, existe alguna cara que, al prolongarla, corta al poliedro.

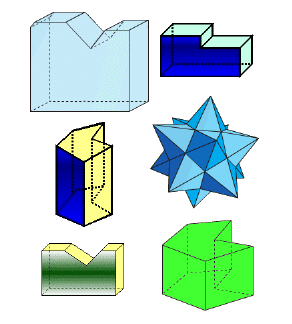Poliedros convexos	Poliedros concavos

 

 En un poliedro convexo se cumple la fórmula de Euler:  CARAS + VÉRTICES = ARISTAS + 2

Según la forma de sus caras

•  Poliedros regulares son aquellos cuyas caras son todas, polígonos regulares iguales, y además en cada vértice se unen el mismo número de caras.
• Polígonos irregulares todos los que no son regulares

 

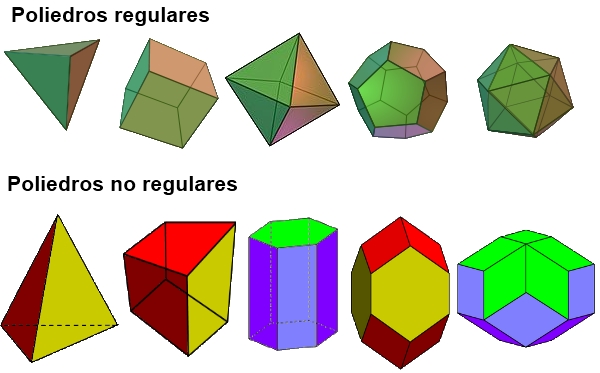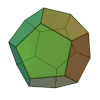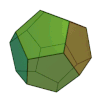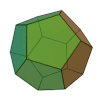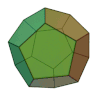
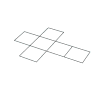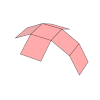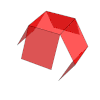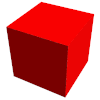
Sólo existen 5 poliedros regulares, también llamados sólidos platónicos:

 

Sólidos Platónicos	Tetraedro	Hexaedro, Cubo	Octaedro	Dodecaedro	Icosaedro
Animación
Desarrollo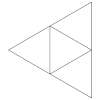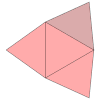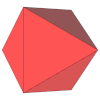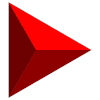
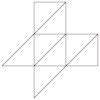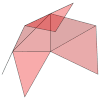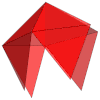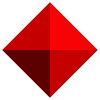Número de caras	4	6	8	12	20
Polígonos que forman las caras	Triángulos Equiláteros	Cuadrados	Triángulos Equiláteros	Pentágonos Regulares	Triángulos Equiláteros
Número de aristas	6	12	12	30	30
Número de vértices	4	8	6	20	12

 Tabla obtenida de la Wikipedia

 Una última clasificación la podemos encontrar debido a la forma de sus caras y a la distribución de estas:

 PROBLEMAS

1. ¿Qué poliedros regulares puedes formar usando como caras cuadrados? ¿Cuántas caras coinciden en cada vértice? ¿Y si usas pentágonos?

2. Comprueba que todos los poliedros regulares verifican la fórmula de Euler.

 

PRISMAS

Un prisma es un poliedro que tiene dos caras que son polígonos iguales y paralelos entre sí, llamadas bases, y sus otras caras laterales son paralelogramos. La altura del prisma es la distancia entre las bases.

Elementos de un prisma

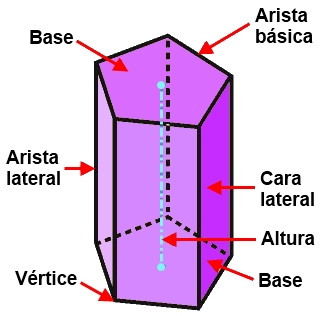Altura de un prisma es la distancia entre las bases. Los lados de las bases constituyen las aristas básicas y los lados de las caras laterales, las aristas laterales; éstas son iguales y paralelas entre sí.

 

Un prisma es recto si las caras laterales son todas rectángulos; es decir, si son perpendiculares a las bases. Cuando no es así, es oblicuo.

Según la forma de las bases, los prismas se clasifican en triangulares, cuadrangulares, pentagonales, etc. Un prisma recto cuyas bases son polígonos regulares decimos que es regular.

 

 

ÁREA DE UN PRISMA 

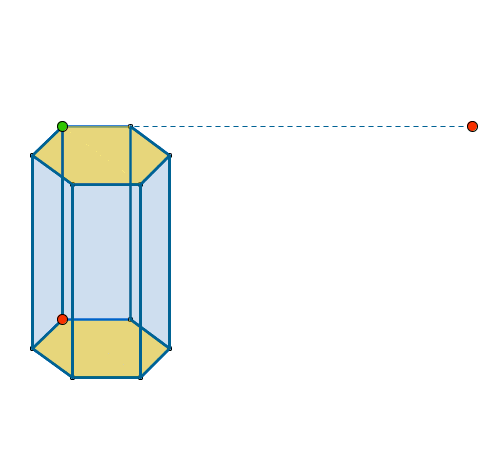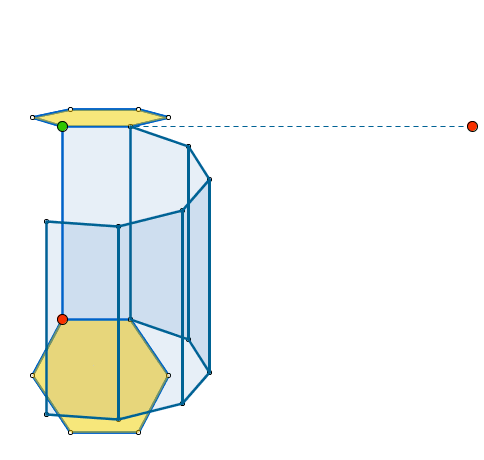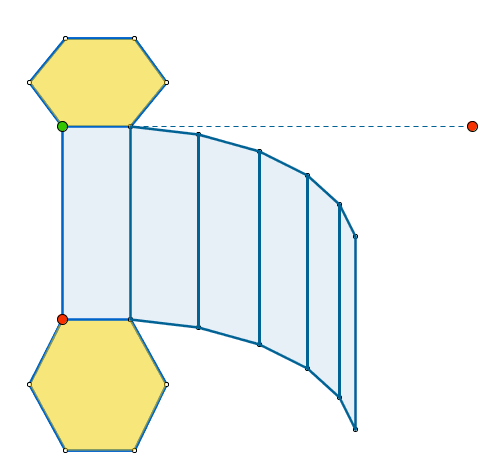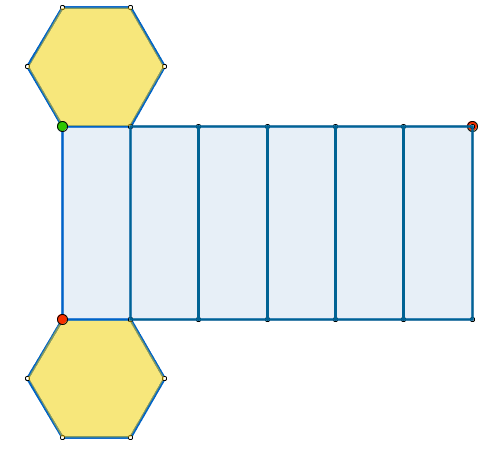Como vemos, este prisma hexagonal tiene 6 caras laterales que son rectángulos y 2 bases que son hexágonos. El área lateral de un prisma es la suma de las áreas de sus caras laterales (los 6 rectángulos). Las 6 caras laterales forman un rectángulo cuya base es el perímetro del hexágono de la base. Por tanto, el área lateral del prisma es igual al producto del perímetro de la base por la altura: Área lateral = perímetro de la base x altura El área total es la suma del área lateral más el área de las 2 bases: Área total = Área lateral + 2 x Área de la base

 VOLUMEN DE UN PRISMA

El volumen de un prisma se puede también definir como el producto del área de la base por la altura, es decir:

V = Área base x altura

Ejemplos:

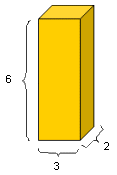	En el ejemplo: V = (3cm x 2 cm) x 6 cm = 6cm² x 6cm = 36cm³
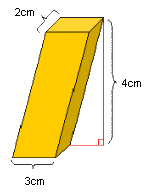	Por ejemplo, si las aristas de la base de un prisma oblicuo miden 3cm y 2cm, y su altura mide 4cm entonces su volumen se calcula a través de la fórmula del prisma recto: V = Área de la base x altura V = (3cm x 2cm) x 4cm = 6cm² x 4cm = 24cm³

 

PROBLEMAS

1. Halla el área total de un prisma hexagonal regular de arista básica 8 cm y altura 10 cm. Halla el volumen de dicho prisma.

2. Calcula la arista de un cubo que tiene igual área total que un ortoedro cuyas dimensiones son 6, 8 y 10 cm. Halla también el volumen de dicho cubo.

3. Calcular el área y el volumen de estos prismas. En ambos la arista de la base mide 3 cm y la altura 4 cm.

   1. a) Prisma hexagonal regular

   2. b) Prisma cuadrangular oblicuo

4. Calcula el área y el volumen de:

   1. Un cubo de arista 12 cm.

   2. b) Un prisma triangular regular de arista de la base 10 cm y altura 6 cm

 

PIRÁMIDES

Una pirámide es un poliedro cuya base es un polígono y cuyas caras laterales son todas triángulos que tienen un vértice común, llamado el vértice de la pirámide.

 La altura es la distancia de este vértice a la base.

Elementos de una pirámide

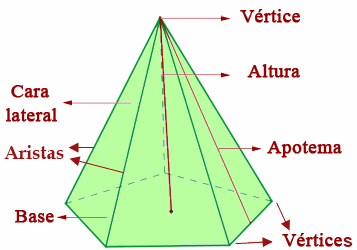Los elementos fundamentales de una pirámide son caras, aristas y vértices.  Las caras pueden ser: - Base de la pirámide, que es un polígono cualquiera. - Caras laterales de la pirámide, que son triángulos. Las aristas pueden ser: - Aristas básicas, que son los lados de la base. - Aristas laterales, que son los lados de las caras laterales que no son aristas básicas. Los vértices pueden ser: - Vértices de la base, que son los vértices del polígono de la base. - Vértice o cúspide de la pirámide, que es el punto en el que se encuentran las aristas laterales. Apotema de una pirámide regular es la altura de cualquiera de sus caras.

Clasificación de pirámides

Una pirámide es recta si sus caras laterales son todas triángulos isósceles. Si no es así, es oblicua.

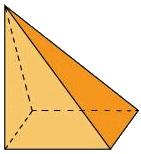Pirámide Recta	Pirámide Oblicua

 

Una pirámide recta con base un polígono regular, decimos que es regular.

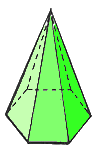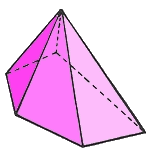Pirámide Regular	Pirámide Irregular

Según el polígono que forma la base, las pirámides son triangulares, cuadrangulares, etc.

AREA DE UNA PIRÁMIDE

Área Lateral = Suma de las áreas de todas sus caras laterales

 Área Total = Área Lateral + Área de la Base

 VOLUMEN DE UNA PIRÁMIDE

 Volumen = 1/3 x Área de la base x Altura 

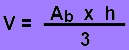 siendo Ab= Área de la base y h=altura

PROBLEMAS

1.  Calcular el área total de una pirámide cuadrangular recta de arista básica 6 cm y altura 4 cm. Calcular también su volumen.
2. Halla el área total de una pirámide hexagonal regular con arista básica 5 cm y apotema de sus caras laterales 12 cm. Calcular también su volumen.

 

CUERPOS REDONDOS

Los tres cuerpos redondos más importantes son el cilindro, el cono y al esfera.

 

CILINDRO

El cilindro es el cuerpo geométrico engendrado por un rectángulo al girar por uno de sus lados.

 

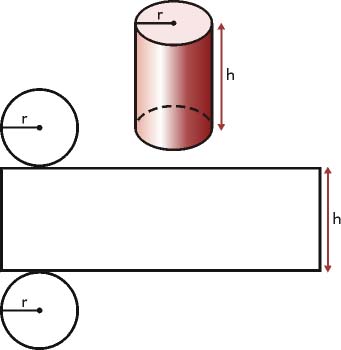
Desarrollo del cilindro

Si desarrollamos un cilindro nos damos cuenta que se descompone en un rectángulo y dos círculos. Llamamos r al radio de la base y generatriz g a la altura del cilindro.

 

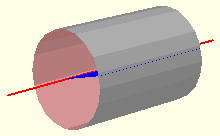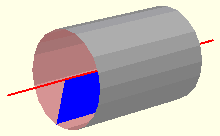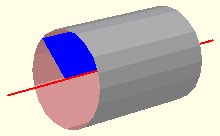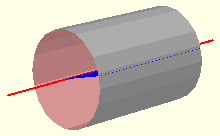
ÁREA DEL CILINDRO

En el desarrollo de un cilindro se aprecia que su superficie lateral es un rectángulo cuya base es igual al perímetro del círculo, 2r, y cuya altura, h, es la del cilindro.

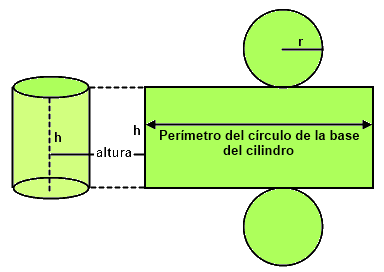Área lateral = Perímetro de la base x Altura = 2 · · r · h  Área total = Área Lateral + 2 · Área de la base = 2 · · r · h + 2 ·· r2

  

VOLUMEN DEL CILINDRO

 Volumen = Área de la base x Altura = · r² · h

 

CONO

El cono es el cuerpo geométrico engendrado por un triángulo rectángulo al girar por uno de sus catetos.

  

Desarrollo del cono

Si desarrollamos un cono nos damos cuenta que se descompone en un sector circular y un círculo que es la base. Llamamos r al radio de la base y generatriz g al radio del sector

  

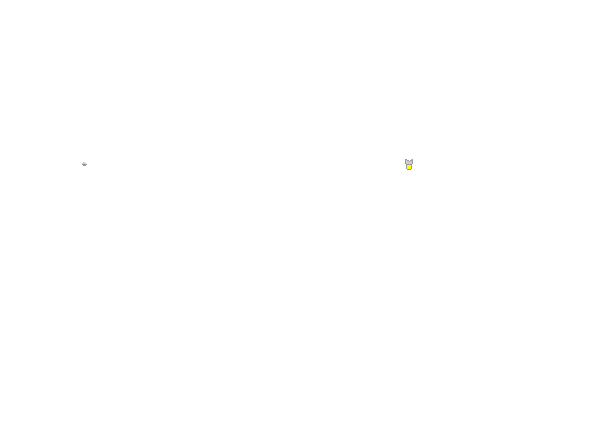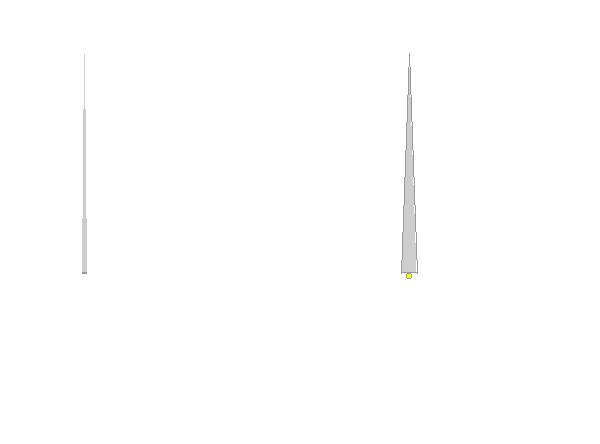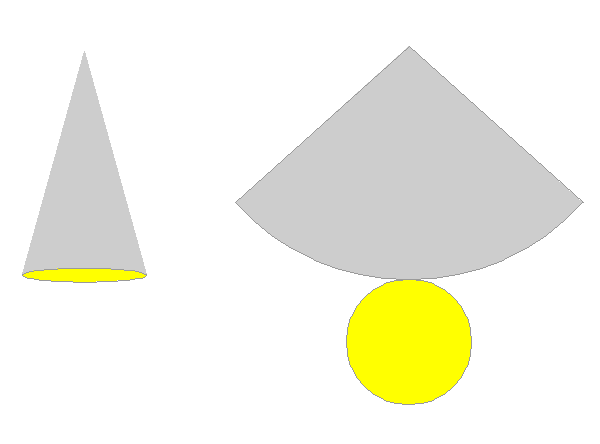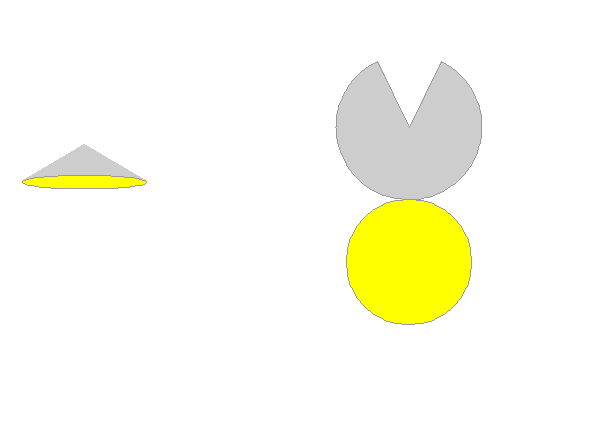
ÁREA DEL CONO

En el desarrollo de un cono recto se aprecia que su superficie lateral es un sector circular de radio g.

¿Qué porción de círculo tiene ese sector? 

 

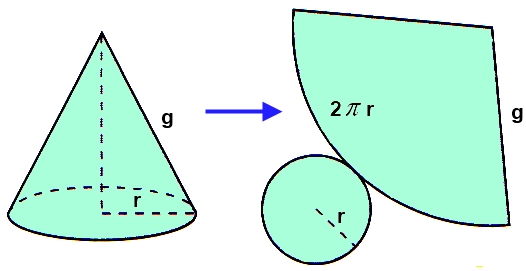
La circunferencia completa tiene una longitud de 2r.

• El sector circular tiene una longitud de 2r.
• El área de la base es r².
• El área del sector circular es: · r · g
  

Área total del cono = Área lateral + Área de la base = r g + r²

 

 VOLUMEN DEL CONO

Al igual que todos los cuerpos geométricos que terminan en un vértice, su volumen es 1/3 del área de la base por la altura

 Volumen = 1/3 · Área de la base · Altura = 1/3 · · r² · h

 ESFERA

La esfera es el cuerpo geométrico engendrado por un semicírculo al girar sobre su diámetro.

 

ÁREA DE LA ESFERA

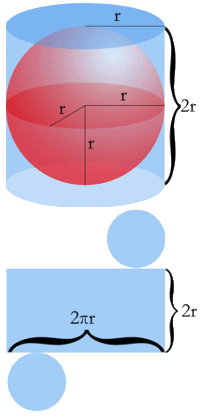Arquímedes demostró que el área de una esfera es igual al área lateral de un cilindro que tenga el mismo radio y cuya altura sea el diámetro de la esfera. La imagen muestra una esfera envuelta por un cilindro que se ajusta por completo a ella, un cilindro de radio R y altura 2R. Tenemos entonces que el área de la esfera es igual al área lateral de ese cilindro: A Esfera = A Lateral del cilindro = 2R x 2R = 4R2

 

VOLUMEN DE LA ESFERA

La esfera solo ocupa las dos terceras partes del volumen del cilindro que la contiene:

V _Esfera = 2/3 V _Cilindro = 2/3 · R² · 2R = 4/3 R³

 PROBLEMAS

1.   Halla el área y el volumen de las siguientes figuras: a) Un cono de radio de la base 7 cm y generatriz 24 cm. b) Un cilindro de radio de la base 4 cm y generatriz 10 cm.
2. . Calcula el área total y el volumen de:
   1. a) Un cono de radio de la base 5 cm y altura 12 cm.
   2. b) Una esfera de radio 10 cm.
   3. c) Un cilindro de radio de la base 6 cm y generatriz 8 cm.

 

 Fuente de las imágenes: Plan Ceibal (http://ceibal.edu.uy/).

Más información:

• Poliedros
• Prismas
• Pirámides
• No poliedros
• Poliedros en educarex