Teoría

Los Números Enteros

El conjunto de los números enteros está compuesto de los números positivos (+1, +2, +3, ...), los negativos (-1, -2, -3, -4, ...) y el cero. El conjunto de los números enteros se representa con la letra Z:

Z= { ...., -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, ....}

Valor absoluto de un número a es el número que resulta al quitar el signo. En un número positivo es el mismo y en los negativos es el mismo número pero en positivo. Se representa como | a |. Ejemplos: | 4 | es 4, | -4 | es 4

El opuesto b de un número entero a es aquel que la suma de ambos es cero. Por lo tanto, el opuesto de cualquier entero es el mismo número cambiado de signo. Ejemplos: Opuesto(4) = -4, Opuesto de (-5)=5

Comparación de números enteros

La comparación de números enteros es muy sencilla teniendo en cuenta lo siguiente:

1. Un número positivo siempre es mayor que uno negativo.
2. El cero es mayor que cualquier negativo y menos que cualquier positivo.
3. En los números positivos ordenamos igual que con los naturales.
4. En los números negativos, es mayor el número con menor valor absoluto  ( de forma sencilla, el que obviando el signo es menor) . Ejemplo: - 2 > - 5

Si pensamos en su representación gráfica en la recta, un número es mayor que otro si está a la más a la derecha en la recta.

Suma y resta de números enteros

Para sumar dos números enteros se hace:

• Si los dos números tienen el mismo signo, se suman sus valores absolutos y se pone el signo que tenían. Ejemplo: ( +5) + (+3) = +8   (-5)+(-3)= -8
• Si tienen distinto signo, se restan sus valores absolutos y se pone el signo del que tiene mayor valor absoluto. Ejemplo: (+5) + (-3) = +2 y (-5) + (+3) =-2

Para restar dos  números enteros se le suma al primero el opuesto del segundo. Ejemplos: (+5) - (-3) = +5 +3 = +8  (+5) - (+3) = +2

Multiplicación y división de números enteros

En ambos casos se sigue el mismo procedimiento:

1. Se multiplican o dividen sus valores absolutos.
2. El signo se decide con la regla de los signos:  + por + = +, + por - = - y - por - = +.

Ejemplos:

• (+3) · (+3) = +9    (+3) · (-3) = -9     (-3) · (-3) = +9  
• (+3) : (+3) = +1    (+3) : (-3) = -1      (-3) : (-3) = +1

 

Potencias de números enteros

Una potencia es una manera abreviada de expresar una multiplicación de factores iguales.

Por ejemplo, 2⁴ es una potencia. Se lee "dos elevado a cuatro" y significa 2·2·2·2. La base es 2, que es el factor que se repite. El exponente es 4, que es el número de veces que se repite la base.

Observa que las potencias más sencillas son las que tienen como base 1 ó 10.

Signo de las potencias

El signo de una potencia de base un número positivo es positivo.

El signo de una potencia de base un número negativo es positivo si el exponente es par y negativo si el exponente es impar. Ejemplos: (-5)²= +5²  (-5)³= +5³

 Propiedades de las potencias

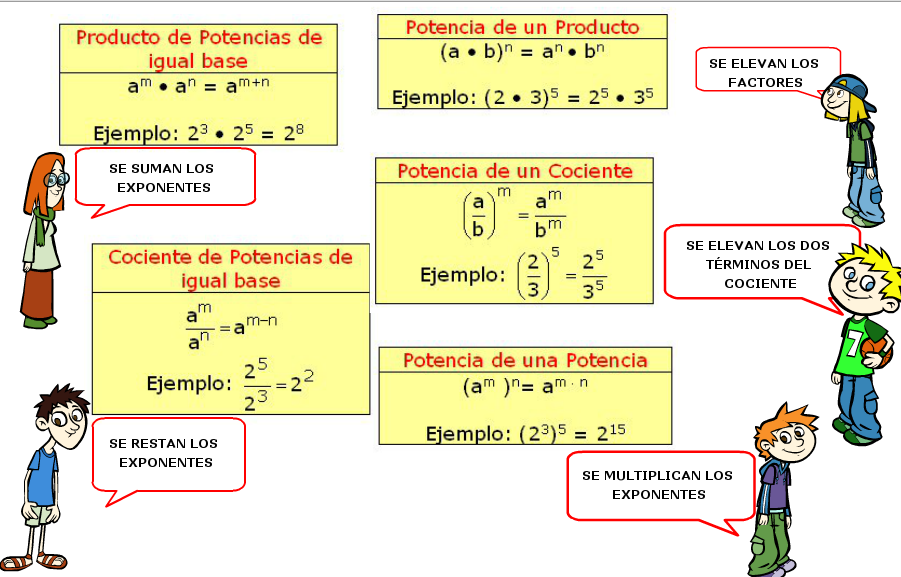
 • Producto con la misma base .Ejemplo: a^m· aⁿ = a^m+n . Ejemplo: 6⁷ · 6⁴ = 6⁷⁺⁴ =6¹¹

 • Cociente con la misma base: a^m : aⁿ = a^m-n.Ejemplo: 6^{7 :} 6⁴ = 6^7-4 = 6³

• Potencia de una potencia: (a^m)ⁿ = a^m·n . Ejemplo: (6⁷ )⁴= 6^7·4 = 6²⁸

• Producto y el mismo exponente:   aⁿ · bⁿ= (a·b)ⁿ .

 • Cociente y el mismo exponente: aⁿ : bⁿ = (a:b)^{n .}

 • Exponente 0: a⁰ = 1

 • Exponente 1: a¹ = a

 

Raíz cuadrada exacta

 

La raíz cuadrada es la operación contraria a elevar al cuadrado. Por ejemplo, la raíz cuadrada de 64 es 8 porque 8²=64 y se escribe √64=8.
El símbolo √  se llama radical y el número que está dentro del radical es el radicando.

 

 Si un número se eleva al cuadrado se obtiene un número cuadrado. Los números cuadrados tienen una raíz cuadrada exacta.

 

 √a=b significa que b²=a

 

√radicando = raíz cuadrada

 

 

Raíz cuadrada entera

Muchos números no tienen raíz cuadrada exacta. En tal caso se calcula la raíz cuadrada entera y habrá un resto.

Por ejemplo, 70 no tiene raíz cuadrada exacta porque 8²=64 y 9²=81. La raíz cuadrada entera de 70 es 8 y el resto es 70−64=6. √70=8 y resto 6.

Para hacer raíces cuadradas por tanteo buscaremos números que al elevarlos al cuadrado se aproximen al radicando.

 

Jerarquía de las operaciones

El orden para realizar operaciones es:

1. Operaciones entre paréntesis
2. Potencias o raíces
   
3. Multiplicaciones y divisiones
4. Sumas y restas

 

 Si solo hay multiplicaciones y divisiones o solo hay sumas y restas, se realizan de izquierda a derecha.

Divisibilidad en los números naturales

Un número es divisible por otro cuando la división entre ellos es exacto, o sea, el resto de la división es cero.

Cuando esto sucede decimos que D es divisible por d. Tenemos que D contiene un número exacto de veces a d.

Ejemplos:

• Si dividimos 48 entre 8, el cociente es 6 y el resto 0. En este caso decimos que 48 es divisible por 8. Y podemos comprobar que 6 veces 8 nos da 48, o sea, el número 48 contiene 6 veces al 8.
• Al contrario, si dividimos 63 entre 4, el cociente es 15 y el resto es 3. Por lo tanto, 63 no es divisible entre 4.

Criterios de divisibilidad

Los criterios de divisibilidad son reglas que nos permiten saber de forma rápida (sin efectuar la división) si un número es divisible por otro.

En la siguiente tabla se pueden ver los principales criterios de divisibilidad:

Divisible por ...	Criterio de divisibilidad
2	La última cifra es par. Ejemplo: 738 ya que 8 es par.
3	La suma de sus cifras es divisible por 3. Ejemplo: 738, la suma de sus cifras es 7+3+8=18 que es divisible por 3.
4	El número que forma las dos últimas cifras es divisible por 4. Ejemplo: 432, sus dos últimas cifras 32 es divisible por 4.
5	La última cifra es 0 ó 5. Ejemplo: 65345, su última cifra es 5.
6	Si es divisible por 3 y 2 a la vez. Ejemplo: 738 ya que divisible por 2 y 3.
7
8	El número que forma las dos últimas cifras es divisible por 8. Ejemplo: 1.104, sus tres últimas cifras 104 es divisible por 8.
9	La suma de sus cifras es divisible por 9. Ejemplo: 738, la suma de sus cifras es 7+3+8=18 que es divisible por 9.
10	La última cifra es 0.Ejemplo: 65340, su última cifra es 0.
11	La diferencia entre la suma de las cifras de lugar par y la suma de las cifras de lugar impar es 0 o divisible por 11.

 Múltiplos y divisores

Un número b es múltiplo de otro a si la división de b entre a es exacta. O lo que es lo mismo, si b es divisible por a. Ejemplos: 45 es múltiplo de 5, también lo sería de 9 y de 3.

Un número a es divisor de otro número b si si la división de b entre a es exacta. 

Los divisores de un número se obtienen dividiendo dicho número entre los sucesivos números naturales hasta que el cociente es menor que el divisor. Por supuesto, el 1 y el propio número siempre son divisores de un número.

Ejemplo: calcular los divisores de 72. 72 es múltiplo de 2 ya que es par. Dividimos 72 entre 2, el cociente es 36. Aplicamos el mismo procedimiento sobre 36, dividimos entre 2, cociente 18. Aplicamos sobre 18, dividimos entre 2, el cociente es 9. Aplicamos al 9, 9 no es divisible entre 2, probamos con 3 que sí lo es. Dividimos 9 entre 3, cociente 3. Aplicamos sobre el 3 que el divisor es el mismo. Por lo tanto, los divisores de 72 son el 2 que lo es 3 veces y el 3 que es 2 veces.

Números primos y compuestos

Un número a es primo si sus únicos divisores son el mismo y la unidad. Ejemplo: 47, divisores 1 y 47.

Un número a es compuesto si tiene más de dos divisores. Ejemplo: 48, divisores {1, 2, 3, 4, 6, 8, 12, 24, 48}

Todos los números se pueden descomponer en factores que es expresarlo en forma de producto. Los números primos solo tienen una descomposición en factores: a= a ·1

Factorizar un número es expresarlo como  producto de factores primos o, dicho de otra manera, descomponerlo en factores primos. Por ejemplo, la factorización de 72 que hemos visto en el ejemplo anterior es 72= 2·2·2·3·3. Generalmente lo expresaremos en forma de potencias, 2·2·2 es 2³ y 3·3 es 3²  y la descomposición es 72= 2³ · 3² .

Máximo común divisor (MCD)

El máximo común divisor de dos o más números es el mayor de los divisores que tienen dichos números en común.

Los divisores de 12 son { 1, 2, 3, 4, 6, 12} y los de 20 son {1, 2, 4, 5, 10, 20}. Por lo tanto, el mayor de los divisores comunes (MCD) es MCD(12, 20) = 4.

Cómo calcular el MCD de dos números:

Pasos a seguir	Ejemplo de MCD de 72 y 48
Hacer la descomposición factorial	Hacemos la descomposición factorial de 72 y 48: 72 = 23 · 32 48 = 24 · 3
Escogemos los factores primos comunes elevados al menor exponente.	Los factores primos comunes son 2 y 3. El menor exponente es 3 para el número 2 y 1 para el número 3. Nos quedamos con 23 y 3.
Multiplicamos los factores con el menor exponente	El MCD(72,48)= 23 · 3= 8·3 = 24

 

Mínimo común múltiplo (mcm)

El mínimo común múltiplo de dos o más números es el menor de los múltiplos comunes a dichos números.

Los múltiplos de 12 son { 12, 24, 36, 48, 60, 72, ...} y los de 20 son {20, 40, 60, 80, 100, ...}. Por lo tanto, el menor de los múltiplos comunes (mcm) es mcm(12, 20) = 60.

Cómo calcular el mcm de dos números:

Pasos a seguir	Ejemplo de mcm de 72 y 48
Hacer la descomposición factorial	Hacemos la descomposición factorial de 72 y 48: 72 = 23 · 32 90 = 2 · 32 · 5
Escogemos los factores primos comunes y no comunes elevados al mayor exponente.	Los factores primos comunes y no comunes son 2, 3 y 5. El mayor exponente es 3 para el número 2, 2 para el número 3 y 1 para el 5 . Nos quedamos con 23 , 32 y 5
Multiplicamos los factores con el mayor exponente	El mcm(72,48)= 23 · 32 · 5 = 8 · 9 · 5 = 360

Recuerda lo más importante

Números naturales • Hay diez cifras o dígitos para formar los números. Cada cifra tiene un valor dependiendo de la posición que ocupe (en el número 3588, la cifra 5 vale 500). • Los números están ordenados y se usa el símbolo < para menor que y > para mayor que. • Redondear un número es sustituir sus últimas cifras por ceros pero observando la primera cifra que se sustituye por si hay que añadir una unidad a la cifra anterior.	Potencias • Una potencia es una multiplicación de factores iguales. El factor que se repite es la base y el exponente es el nº de veces que se repite la base.
Operaciones • En la suma hay sumandos;  en la resta está el minuendo y el sustraendo, y el primero tiene que ser mayor que el segundo; en la multiplicación hay factores; en la división se cumplirá: dividendo = divisor · cociente + resto   (resto<divisor) y si el resto es cero la división es exacta. • Cuando se realicen operaciones combinadas, primero se hacen los paréntesis, después los productos y divisiones, y lo último son las sumas y restas.	Raíz cuadrada • √a=b si b2=a. (a es el radicando y b es la raíz cuadrada). Si no hay raíz exacta, elegimos el mayor número b tal que b2<a, y habrá un resto=a-b2.
	Calculadoras • Antes de usar una calculadora debes saber si es científica (respeta la jerarquía de las operaciones) o estándar (realiza las operaciones en el orden en que se introducen).